wielokąty, figury podobne anna: 1) Na okręgu o promieniu r opisano trapez prostokątny, którego dłuższa podstawa ma długość 3r. Oblicz pole trapezu. 2)Oblicz promieć okręgu wpisanego: a) w trójkąt o obwodzie 30cm i polu 50cm² b) w czworokąt o obwodzie 40cm i polu 60cm² c) w wielokąt o obwodzie 50cm i polu 100cm² 3) Czworokąt ABCD wpisany jest w okrąg. Oblicz promień tego okręgu, jeśłi |AB|=|AC|=4 oraz |BD|=|CD|=6.

anna: 1) Na okręgu o promieniu r opisano trapez prostokątny, którego dłuższa podstawa ma długość 3r. Oblicz pole trapezu. 2)Oblicz promieć okręgu wpisanego: a) w trójkąt o obwodzie 30cm i polu 50cm2 b) w czworokąt o obwodzie 40cm i polu 60cm2 c) w wielokąt o obwodzie 50cm i polu 100cm2 3) Czworokąt ABCD wpisany jest w okrąg. Oblicz promień tego okręgu, jeśłi |AB|=|AC|=4 oraz |BD|=|CD|=6.

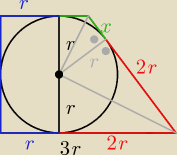
Godzio: Zadanie 1. Z podobieństwa:

x		r
	=
r		2r

	1
x =		r
	2

	3r + 1,5r
P =		* 2r = ...
	2

Godzio: zad 2.

	2P
r =		−− czyli w liczniku masz 2 * pole, a w mianowniku obwód to już sobie
	a + b + c

poradzisz tak samo z pozostałymi

	2P
b) r =
	a + b + c + d

	2P		2 * 100
c) r =		=		= ...
	a + b + c + d + ...		50

jak nie będziesz wiedziała skąd się to bierze to pisz

Anna: Dziękuję, ze mi pomogłeś. Spoko, sama doszłam do tego skądś się co wzięło. Mam nadzieję, ze dzięki temu będzie już coraz mniej kłopotów

Klaudia: Udowodnij, że każda przekątna czworokąta ma długość mniejszą od połowy jego obwodu. Pomóżcie plissss..

pigor: ..., narysuj sobie dowolny czworokąt ABCD i np. przekątną AC, to suma |AB|+|BC|+|CD|+|CA|=2p − obwód tego czworokąta i masz układ 2−óch nierówności (warunków istnienia) trójkąta : |AC|< |AD|+|DC| i |AC|<|AB|+|BC| /+ stronami ⇔ ⇔ 2|AC|< |AD|+|DC|+|AB|+|BC| ⇔ 2|AC|< 2p /:2 ⇔ ⇔ |AC|< p , a to należało wykazać (c.n.w.) −−−−−−−−−−−−−−−−−−−−−−−−−−−− p.s. możesz się ... sprawdzić i analogicznie wykazać to samo dla drugiej BD przekątnej i to tyle; nie jeszcze jedno: na drugi raz zakładaj nowy temat (post) na swoją prośbę,