Okrąg wpisany w kwadrat ABCD o wierzchołkach A(0, 0), B(2, –2), C(4, 0), D(2, 2) olek: Okrąg wpisany w kwadrat ABCD o wierzchołkach A(0, 0), B(2, –2), C(4, 0), D(2, 2) można opisać równaniem:

think: olek okrąg wpisany w kwadrat ma środek w połowie odcinka łączącego przeciwległe boki, a jego promień jest równy połowie długości boku kwadratu.

olek: ja wielm. tylko nie umiem tego opisać równianiem

think: zacznij od narysowanie tego kwadratu w układzie współrzędnych. Umiesz tutaj robić rysunki?

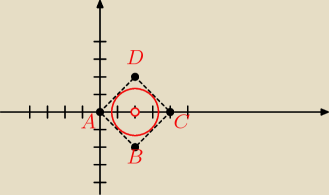
think: Współrzędne środka okręgu to środek odcinka AC lub BD jak kto woli...

AC		0 + 2		0 + 0
	= (		;		) = (1, 0)
2		2		2

|AB| = √(2 − 0)² + (−2 − 0)² = √8 = 2√2

	|AB|		2√2
r =		=		= √2
	2		2

Równanie okręgu: (x − 1)² + y² = (√2)² (x − 1)² + y² = 2

olek: ech. a mnie wyszło tyle (x + 2)² + y² = 2

think: Twój okrąg miałby wtedy środek w punkcie (−2, 0) zauważ że to poza kwadratem.

olek: to już nie wiem. a odpowiedzi do tego zadania to a) (x + 2)² + y² = 2 b) (x + 2)² + y² = 4 c) x² – 4x + y² + 2 = 0 d) x² – 4x + y² = 0.

think: nie mam pojęcia skąd takie odpowiedzi, ale rozwiązania jestem pewna.

olek: no kurcze. tylko, że to jest zadanie ze sprawdzioanu, wiec któreś odp. musi być prawidłowa. nie wiem tylko jak, bo am też nie mogę dojsć

think: olek na Twoim miejscu tak bym się nie przejmowała, bo jeśli nie potrafisz znaleźć błędu w rozwiązaniu, to znaczy, że go tam nie ma! pozdrawiam

Clever : Think źle obliczyłaś środek okręgu Środek okręgu jest równy (2,0) Podstawione do wzoru na równanie okręgu (x−2)² +y² = 2 Czyli odp c) jest poprawna