zadanie tekstowe paziówna: mam problem z takim zadaniem i nie wiem, jak je ugryźć(zadanie z egzaminu z analizy matematycznej z wydziału ekonomicznego): Boisko piłkarskie ma kształt prostokąta o wymiarach 60 m x 100 m. Na środkach krótszych boków znajdują się bramki o szerokości 7 m. Z którego punktu dłuższego boku boiska należy wykonać strzał na bramkę przeciwnika, aby szansa strzelenia gola była największa? Przyjmujemy, że szansa strzelenia gola jest tym większa, im większa jest miara kąta wyznaczonego przez odcinki łączące punkt strzału z podstawami słupków bramki. z góry dziękuję za pomoc

paziówna: ponawiam

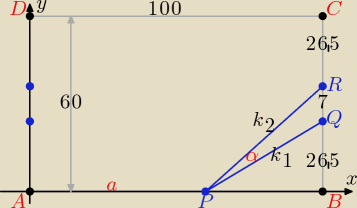
Bogdan: |AB| = |CD| = 100, |AD| = |BC| = 60, |AP| = a > 0, |PB| = 100 − a > 0 |BQ| = |RC| = 26,5, |QR| = 7, |BR| = 33,5 A = (0; 0), P = (a; 0), B = (100; 0), Q = (100; 26,5), R = (100; 33,5)

	26,5
Prosta k1 zawierająca odcinek PQ: y = a1x + b1, a1 =		.
	100 − a

	33,5
Prosta k2 zawierająca odcinek PR: y = a2x + b2, a2 =		.
	100 − a

	a1 − a2
tgα = |		| =
	1 + a1*a2

	26,5   33,5   −   100 − a   100 − a
= |		| =
	26,5   33,5   1 + *   100 − a   100 − a

	7(100 − a)
=
	(100 − a)2 + 26,5*33,5

	7(100 − a)
tgα = f(a) =
	(100 − a)2 + 26,5*33,5

Miara kąta α w podanych warunkach zadania osiągnie maksimum, gdy osiągnie maksimum funkcja f(a). Trzeba więc wyznaczyć maksimum funkcji f(a).

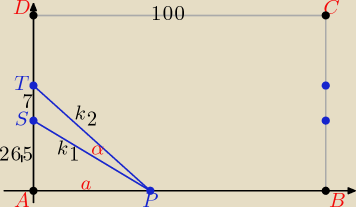Bogdan: Obliczenia są prostsze dla takiego wskazania kąta α jak na tym rysunku i przyjęcia, że prosta k₁: y = a₁x + b₁ zawiera punkty P i S, prosta k₂: y = a₂x + b₂ punkty P i T. P = (a; 0), S = (0; 26,5), T = (0; 33,5)

	26,5		33,5
a1 = −		, a2 = −		,
	a		a

	−26,5   −33,5   −   a   a		7a
tgα = |		| =
	−26,5   −33,5   1 + *   a   a		a2 + 887,75

	7a
Trzeba wyznaczyć maksimum funkcji f(x) =
	a2 + 887,75

Bogdan: Chochlik, chodzi o funkcję f(a), a nie o f(x). Poprawiam.

	7a
Trzeba wyznaczyć maksimum funkcji f(a) =
	a2 + 887,75