Adam: Dla jakicgh wartosci paramatru m, m∊R okregi o rownianiach
o1: x2+y2−2x+2my+m2=0 i
o2: (x−1)2+(y−m)2=m2−4m+4
są zewnętrznie styczne.
Proszę o tłumacznie.
6 wrz 19:33
Adam: zrobi ktos?
6 wrz 22:42
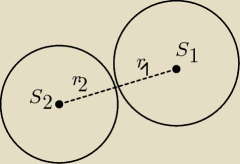
think: Okręgi są zewnętrznie styczne kiedy odległość ich środków od siebie jest równa sumie promieni.
zapisz te równania okręgów w postaci (x − a)2 + (y−b)2 = r2
Policz odległość S1 od S2 i sprawdź czy jest równe r1 + r2
6 wrz 23:16
think:
S
1 = (a
1,b
1)
S
2 = (a
2,b
2)
|S
1S
2| =
√(a2 − a1)2 + (b2 − b1)2
6 wrz 23:19
Adam: zrobiłem tak i wiesz co mi wyszlo?
m=1 v m=3
co przy równianiu okręgu :
o1: (x−1)
2+(y−1)
2=1
o2: (x−1)
2+(y−1)
2=1 (tak, oba są identyczne)
Sam widzisz, ze się pokrywają. Fakt są styczne zewnetrznie, ale we wszystkich punktach

To samo jest w przypadku m=3.
Jakieś pomysły?
6 wrz 23:20
think: dobra sprawdzę to sobie szybciorem na papierze

6 wrz 23:22
Adam: dzięki, czekam

6 wrz 23:23
think: a mi wyszło m = −1...
6 wrz 23:26
Adam: mi wyszło :
|m−2|=−1 v m−2<0
m−2=−1 v −m+2=−1
m=1 v m=3
6 wrz 23:29
think: ale nie są wtedy zewnętrznie styczne...

6 wrz 23:30
think: a skąd masz takie wartości bezwzględne, pomijam to że |a| ≥ 0 więc nigdy nie będzie = −1
6 wrz 23:31
Adam: jak chcesz moge Ci napisać wszystko co wymyśliłem.
6 wrz 23:35
think: O
1: x
2 + y
2 − 2x + 2my + m
2 = 0
(x − 1)
2 + (y + m)
2 = 1
2
S
1 = (1, −m); r
1= 1
O
2: (x − 1)
2 + (y − m)
2 = m
2 − 4m + 4
(x − 1)
2 + (y − m)
2 = (m − 2)
2
S
2 = (1, m); r
2 = |m − 2| (teraz się dopatrzyłam skąd ten moduł

|S
1S
2| =
√(1 −1)2 + (m+m)2 = 2|m|
1 + |m − 2| = 2|m|
6 wrz 23:37
anmario: Najpierw rzeczywiście trzeba przedstawić równania tych okręgów w postaci zaproponowanej przez
Think. Pierwszy jest już w takiej postaci dany, pozostaje drugi:
x2+y2−2x+2my+m2=0
(x−1)2−1+(y+m)2 =0
(x−1)2+(y+m)2=1
i teraz mamy równania dwóch okręgów w postaci:
(x−1)2+(y+m)2=1
(x−1)2+(y−m)2=m2−4m+4
Pierwszy ma środek w punkcie O1(1, −m) i promień r1=1, drugo ma środek w punkcie O2(1,m) i
promień r2=√m2−4m+4
I znowu, zgodnie z ideą Think, aby były zewnętrznie styczne odległość O1O2 musi być równa
r1+r2.
6 wrz 23:38
Adam: o1: (x−1)2−1+(y−m)2−m2+m2=0
o2: (x−1)2 +(y−m)2=m2−4m+4
|o1o2|=r1+r2
o1:(x−1)2+(y−m)2=1
o2:(x−1)2+(y−m)2=m2−4m+4
|o1o2|=√1−1)2+(m−m)2
|o1o2|=0
r1=√1, r2= √(m−2)2 =|m−2|
|o1o2|=r1+r2
0=1+|m−2|
|m−2|=−1
m−2≥0 v m−2<0
m−2=−1v −m+2=−1
m=1 v m=3
6 wrz 23:40
think: no i wszystko jasne, ja się 'walnęłam' przy promieniu Ty Adamie natomiast w liczeniu odległości
środków odcinków

to jesteśmy kwita a zadanie jest rozwiązane

6 wrz 23:41
Adam: Porównując z Waszymi to pochrzaniłem to

6 wrz 23:41
Adam: 
6 wrz 23:41
think: m = − 3 lub m = 1 a to jest poprawne rozwiązanie

6 wrz 23:43
think: oj tam luzik

jak widzisz sama porobiłam błędy

humane errarum est

6 wrz 23:44
Adam: dzięki za pomoc

6 wrz 23:47
think: wpadaj częściej

6 wrz 23:50
think: nic tak człowieka nie ożywia jak kompromitacja

6 wrz 23:50
Adam: co racja, to racja.
Jeszcze jedno pytanko: Jesteś pewny, że m=1 a nie m=−1?
6 wrz 23:52
think: tak jestem pewn
a 
a co nie wychodzi Ci rozwiązanie?
6 wrz 23:53
think: rozpatrz 3 przypadki dla m∊(−∞,0) m∊<0,2> i m∊(2,∞)
6 wrz 23:54
Adam: ah tak, mój błąd, wszystko się zgadza

Jeszcze raz dziękuję za pomoc

Pozdrawiam i życzę dobrej nocy

PS Wybacz, ale Twój nick mnie zmylił

6 wrz 23:58
think: dla m = 1 masz
O
1: (x − 1)
2 + (y + 1)
2 = 1
2
O
2: (x − 1)
2 + (y − 1)
2 = (1 − 2)
2
co Ci tutaj nie pasuje

bo mi się cosik wydaje, że zmieniłeś znak i dlatego wyszło Ci
równanie tego samego okręgu zamiast dwóch różnych.
6 wrz 23:58
think: dobrej nocy


PS wiem, że ta ksywa robi w konia, ale trudno

6 wrz 23:59
iza: no no
7 wrz 08:05
 S1 = (a1,b1)
S2 = (a2,b2)
|S1S2| = √(a2 − a1)2 + (b2 − b1)2
S1 = (a1,b1)
S2 = (a2,b2)
|S1S2| = √(a2 − a1)2 + (b2 − b1)2
 To samo jest w przypadku m=3.
Jakieś pomysły?
To samo jest w przypadku m=3.
Jakieś pomysły?



 |S1S2| = √(1 −1)2 + (m+m)2 = 2|m|
1 + |m − 2| = 2|m|
|S1S2| = √(1 −1)2 + (m+m)2 = 2|m|
1 + |m − 2| = 2|m|
 to jesteśmy kwita a zadanie jest rozwiązane
to jesteśmy kwita a zadanie jest rozwiązane



 jak widzisz sama porobiłam błędy
jak widzisz sama porobiłam błędy humane errarum est
humane errarum est 



 a co nie wychodzi Ci rozwiązanie?
a co nie wychodzi Ci rozwiązanie?
 Jeszcze raz dziękuję za pomoc
Jeszcze raz dziękuję za pomoc  Pozdrawiam i życzę dobrej nocy
Pozdrawiam i życzę dobrej nocy  PS Wybacz, ale Twój nick mnie zmylił
PS Wybacz, ale Twój nick mnie zmylił 
 bo mi się cosik wydaje, że zmieniłeś znak i dlatego wyszło Ci
równanie tego samego okręgu zamiast dwóch różnych.
bo mi się cosik wydaje, że zmieniłeś znak i dlatego wyszło Ci
równanie tego samego okręgu zamiast dwóch różnych.

 PS wiem, że ta ksywa robi w konia, ale trudno
PS wiem, że ta ksywa robi w konia, ale trudno