Zadanie z matematyki, geometria płaska Hanka_: Wysokość trójkąta prostokątnego poprowadzona na przeciwprostokątną podzieliła ją na odcinki długości 18cm i 2 cm. Oblicz długość promienia okręgu wpisanego w ten trójkąt.

Bogdan: Oblicz najpierw długość wysokości tego trójkąta poprowadzonej z wierzchołka kąta prostego.

Hanka_: Wynosi 6 cm. Tylko nie wiem, co dalej.

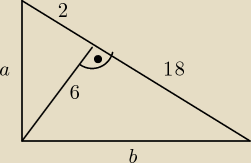
Kejt: Obliczasz pozostałe boki:

	20*6
P=		=60
	2

a*b
	=60
2

a²+b²=20²

Bogdan: Teraz oblicz długości boków trójkąta: a = , b = , c = 18 + 2 = 20

Bogdan:

	1
Długość r promienia okręgu wpisanego można wyznaczyć z zależności: r =		(a + b − c)
	2

Hanka_: Dziękuję serdecznie!

shisha: powinno byc r= ¹₂(a+b+c)

Bogdan:

	1
Uzasadnij shisha podaną zależność r =		(a + b + c), mam nadzieję, że potrafisz.
	2

Bogdan: Nie potrafisz?

brikens: Mam pytanie, wysokość nie powinna wynosić 10 cm ? Dlaczego jemu wyszło 6 ?

brikens: a nie jednak dobrze jest 6, a na wikipedi pisze: Wysokość opuszczona na przeciwprostokątną ma długość , jest ona zarazem średnią geometryczną długości odcinków, na które dzieli przeciwprostokątną spodek wysokości