przestrzen- ogolnie hashiri: ZAD1. Udowodnij, ze dwie plaszczyzny rownolegle przeciete trzecia plaszczyzna przecinaja sie z nia wzdluz prostych rownoleglych. Nie idzie mi tu ten dowod, bo nie potrafie udowodnic rzeczy oczywistych jakby ZAD2. W czworoscianie ABCD punkty P,Q,R sa srodkami odpowiednio krawedzi AD, BD, CD. Udowodnij, ze plaszczyzny PQR i ABC sa rownolegle. Tego poprostu nie moge zrobic Ja rysuje ten czworoscian jakby z podstawa ABC i gornym wierzcholkiem D i mam udowodnic rownoleglosc dwoch trojkatow. Prosze o szybka pomoc.

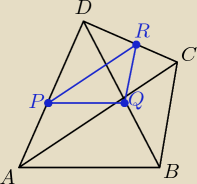
Godzio: Zadanie 2. Dowód opiera się na takim twierdzeniu: Odcinek łączący środki 2 ramion trójkąta jest równoległy do trzeciego boku i jest równy połowie jego długości Wiedząc to możesz udowodnić że płaszczyzny są równoległe

hashiri: Ok wielkie dzieki. Jak to twierdzenie przeczytalem to bez problemu, tylko jak udowodnic to twierdzenie?

Godzio: to co podałem ?

hashiri: tak

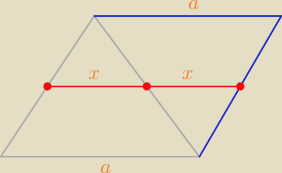
Godzio: Dorysowałem do trójkąta część i powstał nam równoległobok, czerwony odcinek łączy nam środki tego równoległoboku i to już jest dowód że jest równoległy

	1
a = 2x => x =		a
	2

hashiri: Czy ZAD2 to idzie tak: Na podstawie tego Twierdzenia co podales wynika ze boki ABC sa rownolegle to bokow PQR wiec plaszczyzny, na ktorych leza te trojkaty sa rownolegle. Dobrze to zrobilem ?

Godzio: Raczej tak

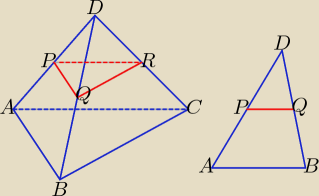
Bogdan: Czy przyda się taki rysunek?

	1
PQ ∥ AB i |PQ| =		|AB|
	2

Analogicznie rozpatruje się pozostałe ściany boczne ostrosłupa.

hashiri: Dzieki, a to pierwsze zadanie, to jak zaczac, bo to takie jakies dziwne i oczywiste, ze nie wiem jak to udowodnic na papierze ?