tryg dario: Dla pewnego kąta ostrego x wiemy ze tgx=3. Oblicz sin4x

anmario: sin4x=sin(2*2x) = 2sin(2x)cos(2x) = 2*2sinxcosx*2sinxcosx=8sin²xcos²x=8sin²x(1−sin²x)=8(sin²x−sin⁴x) i teraz wystarczy z podanej w zadaniu zależności obliczyć sin²x i podstawić do przekształconego w ten sposób wyrażenia na sin4x

anmario: Pochrzaniłem, sorry, zaraz poprawię

anmario: sin4x=sin(2*2x) = 2sin(2x)cos(2x) = 2*2sinxcosx*(cos²x−sin²x)=4sinxcos³x−4sin³xcosx Teraz z zależności tgx=3 trzeba wyliczyć sinx i cosx i podstawić do powyższego wyrażenia. Wykorzystane wzory: sin2x=2sinxcosx cos2x=cos²x−sin²x

dario: dzięki

dario: kurcze wyszło mi −96 a w odp mam −0,96. skąd ten błąd ?

dario: mam taką postać 12cos⁴x−108cos⁴x i nie wiem jak z tym dalej ?

Godzio: tgx = 3 sinx = 3cosx sin²x + cos²x = 1 10cos²x = 1

	1
cos2x =
	10

4sinx*cos³x − 4sin³x*cosx = 12cos⁴x − 4 * 27cos⁴x = cos⁴x(12 − 108) = −96cos⁴x = −96 * (cos²x)² = ...

dario: no tylem wiem ale dalej jak z tym można

Godzio:

	1		1		1
cos2x =		więc (cos2)2 =		, a −96 *		to −0,96 prawda ?
	10		100		100

dario: no fakt

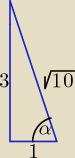
Bogdan: Alternatywne rozwiązanie: α jest kątem ostrym.

	3		1
sinα =		, cosα =
	√10		√10

sin4x = 2sin2x cos2x = 2*2sinx cosx (cos²x − sin²x) =

	3		1		1		9		3		−8		96
= 4*		*		*(		−		) = 4*		*		= −
	√10		√10		10		10		10		10		100