równania z parametrem bas8900: 1.Dla jakich wartości a zbiorem wartości trójmianu: a) y=(1−a²)x²+2(1−a)x−2 b) y=(a−1)x²+(a−1)x+a c) y=−x²+2ax+a−2 jest R_u{0} 2.Dla jakich wartości k zbiorem wartości funkcji: a) y=x²−(2+k)x+1 b) y=kx²−4x+k+3 c) y=(2k−3)x²+(6−k)x+^k−9₇ jest R+u{0} 3.Dla jakich wartości patametru m równanie x²−2mx+m²−1=0 ma dwa rozwiązania należące do przedziału<−2;4> Wogóle nie wiem jak zrobić te zadania bardzo Was prosze pomóżcie

Godzio: 1 i 2 niezbyt rozumiem o co chodzi 3. muszą być spełnione warunki: Δ ≥ 0 f(−2) ≥ 0 f(4) ≥ 0

Godzio: Może Ci napiszę o tym zbiorze to sama pokombinujesz Zbiór wartości funkcji f(x) = ax² + bx + c dla a > 0 to: <q,∞) dla a < 0 to: (−∞,q> gdzie q to 2 współrzędna wierzchołka paraboli który możemy policzyć ze wzoru:

	−Δ
q =
	4a

bas8900: Nie rozumiem mozesz jasniej albo rozwiaz cale prosze

Godzio: mówisz o 3 ? bo w 1 i 2 nie rozumiem tak jak wyżej już napisałem

bas8900: Tak mowie o 3

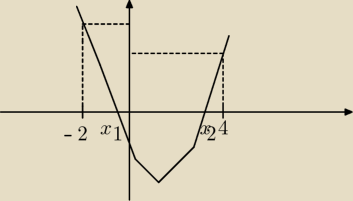
Godzio: ... ma dwa rozwiązania −− to nam sugeruje że musi być warunek: Δ ≥ 0 Teraz ten warunek: f(−2) i f(4) ≥ 0 jak widać na wykresie zeby miejsca zerowe znajdowały się w tym przedziale to muszą być spełnione te 2 warunki. Teraz jest to zrozumiałe ?

Bogdan: Tak zrozumiałem treść zadań 1 i 2: 1. Dla jakich wartości a zbiorem wartości trójmianu jest zbiór R₊∪{0}, czyli zbiór liczb rzeczywistych x ≥ 0. 2. Dla jakich wartości k zbiorem wartości funkcji jest zbiór R₊∪{0}, czyli zbiór liczb rzeczywistych x ≥ 0.