tryg dario:

	π
|cosx|(cosx−cos		)≥0 dla x∊[−π,π] : jeszcze jedno zadanko
	4

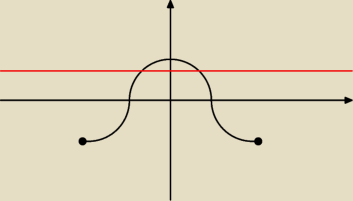Godzio: Nie jestem pewien czy tak można ale myślę że tak: |cosx| ≥ 0 dla x ∊ R więc jedynie co to:

	π
cosx − cos		≥ 0 i to trzeba rozwiązać
	4

	π
cosx ≥ cos
	4

	π		π
x ∊ [		,−
	4		4

dario:

	−π		π		−π		π
w odpowiedziach mam x∊{		,		} ∪ <		,		> nie rozw. takich przykladów z
	2		2		4		4

wart bezw, więc nie mam pojęcia jak to się robi.

Godzio:

	π		π
no tak, dochodzą do tego jeszcze miejsca zerowe |cosx| czyli		i −		bo w innch
	2		2

przypadkach to ten nawias musi być ≥ 0

dario: a jest jakaś ogólna metoda na takie równania z wart.bezw ?

Godzio: mógłbyś też rozpatrzeć przypadki kiedy cosx ≥ 0 => |cosx| = cosx i cosx < 0 => |cosx| = −cosx i wtedy rozwiązywać nierówność może bardziej Ci to podejdzie

dario: chyba rozumiem ale jak być mi podał jakiś przykład nierównosci |cox|*y<0 lub rozw. ten przykład co wcześniej Ci napisałem dla < 0 to bym juz był pewien jak to się robi.

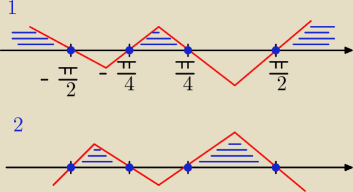Godzio: w takim razie: 1:

	π		π
cosx ≥ 0 ⇒ x ∊ <−		,		> ⇒ |cosx| = cosx
	2		2

	π
cosx(cosx − cos		) ≥ 0
	4

	π		π		π		π
x = −		v x =		v x =		v x = −
	2		2		4		4

	π		π
Rozwiązanie patrzymy tylko w danym przydziale − <−		,		> więc odpowiedź do tego
	2		2

będzie:

	π		π		π		π
x ∊ <−		,		> ∪ {−		,		}
	4		4		2		2

2:

	π		π
cosx < 0 ⇒ x ∊ <−π,−		) ∪ (		,π> ⇒ |cosx| = − cosx
	2		2

	π
−cosx(cosx − cos		) ≥ 0
	4

I jak widać w danym przedziale nie ma żadnego rozwiązania: x ∊ ∅ Końcowa odpowiedź jest sumą przedziałów w każdym rozwiązaniu, w tym wypadku odpowiedzią jeszcze początkowe rozwiązanie

	π		π		π		π
x ∊ <−		,		> ∪ {−		,		}
	4		4		2		2