Proszę o pomoc w zadaniu Marta: Oblicz pole obszaru ograniczonego prostymi: x = 1, x = 2 oraz wykresami funkcji: y =ln x y= e^2x

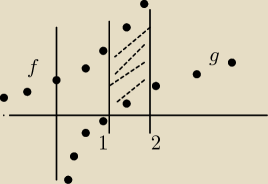
AS: f: funkcja y = e^2x g: y = lnx Szukane pole to pole obszaru między wykresami f i g w przedziale <1,2>. Wyznaczam najpierw całki nieoznaczone. f: J1 = ∫e^2xdx Podstawienie: 2x = t 2dx = dt dx = dt/2 J1 = 1/2∫e^tdt = 1/2e^t = 1/2e^2x g: J2 = ∫lnxdx całkowanie przez części u = lnx dv = dx du = dx/x v = x J2 = u*v − ∫vdu = x*lnx − ∫x*dx/x = xlnx − ∫dx = xlnx − x Obliczam pole P = P1 − P2 = 1/2e^2x[1,2] − (xlnx − x)[1,2] P = (1/2e⁴ − 1/2e²) − ((2ln2 − 2) − (1ln1 −1)) P = 1/2(e⁴ − e²) − 2ln2 + 2 − 1 P = 1/2(e⁴ − e²) − 2ln2 + 1

xxx: można ewentualnie policzyć całke podwójną z 1 po zaznaczonym na rysunku obszarze, ale generalnie na to samo wychodzi