z parametrem trzy zadanka, proszę o pomoc OlciaOlcia93: Trzy zadanka, proszę o pomoc. 1. Dla jakich wartości parametru m równanie |x−2|=|4−3m|−1 ma dwa różne pierwiastki jednakowych znaków. 2. Zbadaj dla jakich wartości parametru m punkt przecięcia prostych mx+(2m−1)y−3m=0 i x+my−m=0 należy do prostokata ABCD, gdzie A=(−1;−2) B=(1;−2) C=(1;2) D=(−1;2) ? 3. Dla jakich wartości parametru m punkt przecięcia prostych mx+4y=−4 i x+my−m−4=0 ma obie współrzędne niedodatnie.

b.: 1. proponuję geometrycznie (na osi liczbowej): co to jest |x−2|? 2. punkt przecięcia prostych = punkt, który spełnia równocześnie równania obu prostych −−> czyli trzeba układ równań rozwiązać 3. jw.

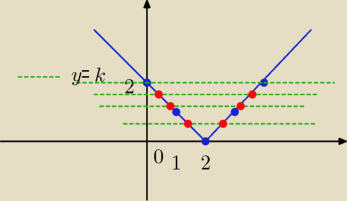
Eta: zad. 1/ równanie: |x−2|= |4−3m| −1 = k dla , k>0 proste ( zielone) : y= k mają dwa punkty wspólne (o dodatnich odciętych , czyli tego samego znaku) tylko wtedy , gdy k€ ( 0, 2) zatem równanie |x−2| = I 4−3m|−1 ma rozwiązania spełniające warunki zad. dla: 0< |4−3m |−1 <2 rozwiąż tenukład nierówności i podaj wartość "m" |4−3m < 3 i |4−3m|> 1 dokończ.........

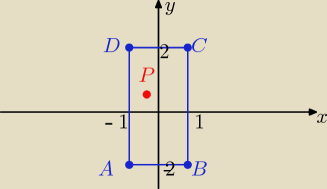
Eta: zad. 2/ Punkt P( x, y) należy do tego prostokąta jeżeli: (*) : −1 ≤ x ≤1 i (**) : −2 ≤ y ≤2 Rozwiąż układ równań tych prostych ( najłatwiej metodą wyznaczników) Otrzymasz:

	m(m+1)
x=
	(m−1)2

	m(m−3)
y=
	(m−1)2

przy założeniu m ≠1 ( bo tylko wtedy proste mają punkt wspólny) nałóż powyższe warunki (*) (**) i rozwiązująac układ takich nierówności podaj cz. wspólną obydwu rozwiązań odp: m€ ( −∞, ¹₃) zad. 3/ podobnie liczby niedodatnie to liczby ≤0 rozwiąż układ równań dany tymi prostymi, otrzymasz : P(x,y) oraz: P(x,y) spełnia warunki zadania, jeżeli: x ≤0 i y ≤0 rozwiąż ten układ nierówności i podaj przedział, do którego należy parametr "m" powodzenia .....