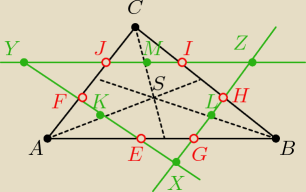
Udowodnij przystawanie trójkątów. Kto ze mną poklika? Patrycja: Zadanie 2. (4.78) Kurczab I kl. zbiór zadań. Punkt S jest środkiem ciężkości trójkąta ABC, punkty K, L, M są odpowiednio środkami odcinków SA, SB, SC. Przez punkt K przeprowadzono prostą równoległą do boku BC, przez punkt L równoległą do boku AC i przez punkt M równoległą do boku AB. Proste te przecinają się w punktach A1, B1, C1. Udowodnij, że ΔABC jest przystający do ΔA1B1C1. Proszę, jest ktoś z kim mogę poklikać o tym zadaniu?

całka nieoznaczona: Niech prosta przechodząca przez punkt K przecina boki AB i AC trójkąta ABC kolejno w punktach E i F, prosta przechodząca przez punkt L przecina boki AB i BC w punktach G i H i podobnie trzecia prosta: w punktach I i J. Rozważ równoległoboki EBiA1 i inne, z których wynika cecha podobieństwa kkk. Następnie z twierdzenia Talesa zastosowanego do kąta BAC i odpowiednich prostych wynika, że skala podobieństwa to jeden.

Patrycja: Witam, już sobie to oglądam na rysunku... Zamieszczam nim zawiesi się mój komputer...

Patrycja: Narysowałam, przepadło przy odświeżaniu strony , więc opiszę co wywnioskowałam Boki AB, BC i CA są podzielone na 3 rowne części każdy. AK do AA1 jest jak AE do AB i to jest 1/3 Stąd widać że każdy mały trójkąt ma swój duży odpowiednik w skali 1 do 3, ale chyba zboczyłam ze ścieżki rozwiązania... Jeśli każdy bok jest podzielony na 3 to AB=YZ, AC=XZ oraz YX=CB. Cecha przystawania trójkątów bbb jest spełniona. Koniec. Poprawnie?

b.: Mnie to nie przekonało do końca. Z tego, co napisałaś wynika, że np. trójkąt XEG jest podobny do ABC w skali 1:3, oraz XEG jest podobny do XYZ, ale nie wiadomo w jakiej skali nie jest dla mnie jasne, skąd wnioskujesz, że np. XEG jest podobny do XYZ w skali 1:3 (bo tak rozumiem ,,każdy mały trójkąt ma swój duży odpowiednik w skali 1 do 3'') p.s. to ,,AK do AA1 jest jak AE do AB'' −− zgadza się, o ile A1 jest środkiem boku BC

Timiusz: makapaka xDπΔΔΩΩΩΩΩ⇒