Ratownik szakal: Ratownik ma do dyspozycji linę i chce przy brzegu plaży wytyczyć kąpielisko dla dzieci w kształcie prostokąta o największej powierzchni. Jakie wymiary powinno mieć kąpielisko, jeżeli lina ma długość: a) 100 m, b) 4a ?

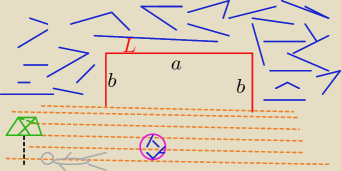
Eta: L= 2b+a= 100m => a = 100−2b , bó ( 0,50) P= a*b = (100−2b)*b= −2b²+100b −−−−− f. kwadratowa , ma max.

	−100
dla bmax=		= 25 m
	−4

to: a_max = 100*2*25= 50 m

Godzio: Heh, Ten ludzik to trup ?

Eta:

Eta: To mulat na plaży

szakal: mulat czy trup, koleś ma 25 metrów wzrostu jeżeli dobrze rozumiem rozwiązanie

Eta: W zad. było pytanie o wymiary kąpieliska ( a nie plażowicza kąpielisko ( czerwona lina) ma wymiary: 25m, 25m, 50 m

think: Eto pisałam Ci już, że jesteś BOSKA, ale takie komplementy należy powtarzać, już mi się humor poprawił

Eta: .........

szakal: Próbowałem sam do tego dojść i mam problem: −2b²+100b b²= −2 b= 100 Δ=10000−4 * (−2) * 0 = 10000 √Δ = 100 x₁ = w liczniku −100 −100= 200 podzielone na 4 z mianownika daje 50 Gdzie robię błąd?

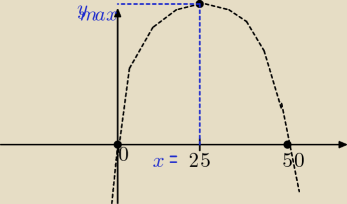
think: szakal, tu nie chodzi o miejsca zerowe, ale o max funkcji, a funkcja kwadratowa ma max jeżeli a < 0, to wtedy max to jej wierzchołek wzór na współrzędne wierzhołka poszukaj i z niego policz.

think:

szakal: Ok już kumam, a przykład b), o co chodzi z "a" mam coś podstawić?

think: nie, 4a to jest po prostu jakaś liczba tylko nie wiesz jaka, rozwiązuj to jak dla punktu a) tylko wyjdzie Ci rozwiązanie zależne od tego a.

Amel: dlaczego 100 * 2 * 25=50? przecież to jest 5000

Eta: tam wkradł mi się chochlik a= 100 −2b => a= 100− 2*25 = 50