Równania kwadratowe z modułem.
lemurek: Równania kwadratowe z modułem.
Możecie mi przykładowo rozwiązać jeden przykład równania kwadratowego z modułem lub napisać co
poklei robić by dojść do wyniku. Wprawdzie mam jakąś koncepcje na rozwiązanie, ale oparta jest
aż na 5 przedziałach, więc trochę dużo i można się łatwo pogubić

Nie mam takiego czegoś w
podręczniku i nie wiem jaki jest najszybszy sposób na rozwiązanie... nie wiem także jak czy
dobrze te przedziały ze sobą łącze (szczególnie gdy wyglądają one mniej więcej tak jak w
przypadku poniżej x∊(−
∞;−2>∪<2;
∞) i x∊(−
∞;−
√5>∪<
√5;
∞))
Weźmy np. taki przykład:
|x
2−4|+|x
2−5|=1
29 sie 19:19
lemurek: A tak BTW. mogą być takie przykłady na maturze 2011? Bo może się niepotrzebnie nad tym głowię

29 sie 19:25
think: będą 3 przypadki
1o gdy x2 − 4 ≥ 0 i x2 − 5 ≥ 0 ⇒ x∊<−∞,−√5) u (√5,∞>
wtedy:
x2 − 4 + x2 − 5 = 1 ← rozw. równanie kwadratowe, sprawdzasz czy pierwiastki należą do
przedziału dla którego rozpatrujemy przedział.
2o gdy x2 − 4 < 0 i x2 − 5 < 0 ⇒ x∊(−2,2)
−x2 + 4 + x2 − 5 = 1 ← tu mamy równanie sprzeczne, więc nie ma rozwiązań
3o gdy x2 − 4 ≥ 0 i x2 − 5 ≤ 0 ⇒ x∊<−√5,−2> u <2,√5>
x2 − 4 − x2 + 5 = 1 ← tu jest tożsamość, więc jest spełnione dla wszystkich x z tego
przedziału.
gdybyś narysował sobie rysunek, to zobaczysz te przedziały.
29 sie 19:30
lemurek: OK, teraz rozumiem..niestety mam kolejny problem − jak się robi przykłady tego typu;
|x2−|x|−2|>2
29 sie 21:56
TOmek : think nieskonczonośc jest przeciez zawsze
) otwarta, przecie

29 sie 21:58
Eta:
1/ x2 −IxI −1 >2 lub x2 −IxI −2 < −2
(*) x2 −IxI> 3 lub x2 −IxI < 0 −−−− sprzeczność
rozpatrz przypadki dla (*)
1/ x ≥0
2/ x <0
dokończ.....
29 sie 21:59
think: cóż najwygodniej byłoby stwierdzić, że rozpatrzmy to dla x ≥ 0 ponieważ oś y−ów będzie osią
symetrii tej funkcji.
29 sie 22:01
lemurek: Próbuje to podejść z różnych stron..a tu bęc... podstawowe przekształcenie

Wielkie dzięki

29 sie 22:02
think: TOmek zgadza się w złym miejscu powstawiałam te nawiasy

jestem dziś normalnie niezła...
29 sie 22:02
think: Eto a:
| | 1 | |
x2 − |x| < 0 jest sprzeczne dla x = |
| ? |
| | 2 | |
29 sie 22:03
Eta:
No tak masz rację

więc trzeba rozpatrzeć dla 1/ x≥0 i 2/ x<0
dla obu tych nierówności
i jako odp: podać sumę rozwiązań

29 sie 22:06
Eta:
Zpomniałam o
ułamkach 
29 sie 22:07
think:
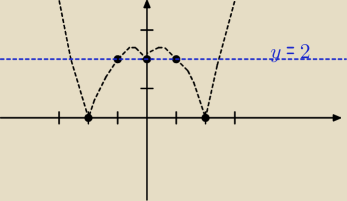
także ja bym zrobiła to tak:
x ≥ 0
|x
2 − x − 2| > 2
Δ = 1 + 8 = 8
√Δ = 3
| | 1 − 3 | |
X2 = |
| = −1 odpada bo x ≥ 0 |
| | 2 | |
| | 1 + √17 | | 1 + √17 | |
Także odpowiedzią byłoby x∊(−∞,− |
| ) u (−1,0) u (0,1) u ( |
| , ∞) |
| | 2 | | 2 | |
29 sie 22:17
think: dobra jest

zmykam, jutro nowy tydzień roboczy czas zacząć, także warto się wyspać.

i
do następnego razu.
29 sie 23:06
 Nie mam takiego czegoś w
podręczniku i nie wiem jaki jest najszybszy sposób na rozwiązanie... nie wiem także jak czy
dobrze te przedziały ze sobą łącze (szczególnie gdy wyglądają one mniej więcej tak jak w
przypadku poniżej x∊(−∞;−2>∪<2;∞) i x∊(−∞;−√5>∪<√5;∞))
Weźmy np. taki przykład:
|x2−4|+|x2−5|=1
Nie mam takiego czegoś w
podręczniku i nie wiem jaki jest najszybszy sposób na rozwiązanie... nie wiem także jak czy
dobrze te przedziały ze sobą łącze (szczególnie gdy wyglądają one mniej więcej tak jak w
przypadku poniżej x∊(−∞;−2>∪<2;∞) i x∊(−∞;−√5>∪<√5;∞))
Weźmy np. taki przykład:
|x2−4|+|x2−5|=1


 Wielkie dzięki
Wielkie dzięki 
 jestem dziś normalnie niezła...
jestem dziś normalnie niezła...
 więc trzeba rozpatrzeć dla 1/ x≥0 i 2/ x<0
dla obu tych nierówności
i jako odp: podać sumę rozwiązań
więc trzeba rozpatrzeć dla 1/ x≥0 i 2/ x<0
dla obu tych nierówności
i jako odp: podać sumę rozwiązań


 także ja bym zrobiła to tak:
x ≥ 0
|x2 − x − 2| > 2
Δ = 1 + 8 = 8
√Δ = 3
także ja bym zrobiła to tak:
x ≥ 0
|x2 − x − 2| > 2
Δ = 1 + 8 = 8
√Δ = 3
 zmykam, jutro nowy tydzień roboczy czas zacząć, także warto się wyspać.
zmykam, jutro nowy tydzień roboczy czas zacząć, także warto się wyspać.  i
do następnego razu.
i
do następnego razu.