Trygonometria Maciek: 1.Analizując wykresy odpowiednich funkcji trygonometrycznych,określ znak liczby: a) sin100^o − sin200^o b)tg 1 + cosπ Nie mam pojęcia , pomóżcie 2.Oblicz : a) cos 720^o cos 720^o= cos(8*90^o)=cos 0^o? Z redukcji której się uczyłem zawsze w nawiasie była zapisana wielokrotność 90^o + jakiś kąt , ale tutaj nie ma nic więc cos 0^o?Coś mi nie pasuje...Reszta przykładów z redukcji mi wyszła okey , a tu nie wiem

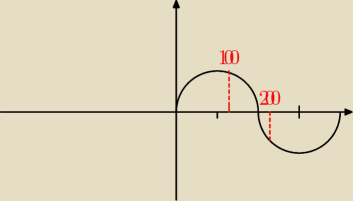
Godzio: sin100 > 0 sin200 < 0 => −sin200 > 0 sin11 − sin200 > 0 analogicznie po wykresie zobacz tg i cos180 powinieneś znać cos(720) = cos(8 * 90 + 0^o) = cos0 = 0

Gustlik: ad 1) a) sin100^o − sin200^o sin100^o=sin(90+10)^o=cos10^o →kofunkcja bo 90^o i znak +, bo w II ćw. sinα>0 sin200^o=sin(270−70)^o=−cos70^o →kofunkcja bo 270^o i znak −, bo w III ćw. sinα<0 sin100^o − sin200^o=cos10^o−(−cos70^o)=cos10^o+cos70^o>0, bo oba cosinusy są dodatnie. b) tg1 + cosπ = tg1+cos180^o=tg1+0=tg1 >0, bo 1 rad≈57^o →kąt I ćw., więc tgα>0 cosπ=cos180^o=0 ad 2) Ja bym to rozpisał tak: cos720^o=cos(2*360^o)=cos0^o=1, a nie 0. [C[Wyjaśnienie tej metody jest tutaj] https://matematykaszkolna.pl/forum/forum.py?komentarzdo=430 To taka moja "skrócona" pamięciowa metoda wyprowadzania wzorów redukcyjnych: reguła kofunkcji + wierszyk o znakach funkcji w ćwiartkach układu współrzednych, bo łatwiej jest zapamiętać dwie proste reguły i szybko wyprowadzić potrzebny w danym zadaniu wzór, niż zapamiętać kilkadziesiąt wzorów redukcyjnych.

Gustlik: Godzio, cos 0^o=1, a nie 0. Pomyliłeś z sinusem.

Maciek: tylko cos(720^o) mam w odp. = 1 ?

Gustlik: Bo ma być 1.

Maciek: Ok tego nie wiedziałem , a sin 0^o = 0?

Godzio: No tak zmęczony dzisiaj i wykresy pomyliłem

Godzio: Maciek spróbuj w myślach wyobrazić sobie wykres sin i cos i po nich sprawdzić sobie wartości dla 0 90 180 270 360 ...

Maciek: Tylko najpierw to się muszę nauczyć jak one wyglądają...

Jasiek: Gustliku cosπ = cos180^o ≠ 0, bo cosπ = −1 tg1 + cosπ = tg1 − 1 > tg45^o − 1 > 0, tg1 > tg45^o

Jasiek: a) sin100^o − sin200^o = sin100^o − sin(2*100^o) = sin100^o − 2sin100^ocos100^o = = 2sin100^o(1/2 − cos100^o) = 2sin100^o * (cos60^o − cos100^o) = = 2sin100^o * 2sin80^o * sin20^o > 0 sin100^o > 0, sin80^o > 0, sin20^o > 0

Godzio: Wszyscy macie 0 pkt nie stosujecie się do polecenia w którym jest wyraźnie napisane że "Analizując wykresy ..."

Jasiek: cos720^o = cos(360^o + 360^o) = cos360^o = 1

think: Jasiek nie przekombinowałeś tego aż nadto? nie wystarczy stwierdzić, że sinus jest dodatni na przedziale x ∊ (0,π) a ujemny dla x ∊ (π, 2π) czyli sin200 < 0 co za tym idzie dwa minusy dają plus sin200 = −a; a > 0 sin100 = b; b > 0 b − (−a) = b + a > 0

Jasiek: a co to za matematyczne stwierdzenie: "dwa minusy daja plus?"

think: niematematyczne, ale dobrze znane iloczynem dwóch liczb ujemnych jest liczba dodatnia.

think: zresztą nie odwracaj kota ogonem, przekombinowałeś i tyle

Eta: Słuszna uwaga Godzio Należy stosować się do polecenia podanego w zadaniu !

Gustlik: Faktycznie, Jasiek, poprawiałem Godzia, a mi się też trafiła pomyłka. Cos 180^o=−1, masz rację.

Maciek: Think ,a mogę wiedzieć co oznacza zapis sin200=−a i sin100=b? Bo to dlaczego sin200<0 i sin100>0 to rozumiem Czy "a" to poprostu kąt ujemny i "b" to kąt dodatni?I po prostu jeden kąt jest oznaczony jako "a" , a drugi jako"b" ?

think: sinus przyjmuje wartości <−1,1> a to liczba z przedziału (0,1] chodzi o to, że sin200 to jest jakaś konkretna wartość tak jak sin100, ale wiemy jedno sin100 ≠ sin200 stąd a i b. Chodziło mi o to aby było widać, że suma tych wartości będzie liczbą dodatnią.

Maciek: A jak zrobić to drugie z tg 1? bo to ,że cosπ = −1 to odczytuje z wykresu.

think:

	sinx
tgx =
	cosx

	sin1
tg1 =
	cos1

przy czym sin1≈0 a cos1≈1 także tg1 ≈ 0 takie oszacowanie teraz tg1 + cosπ ≈ 0 + (−1) ≈ −1

Maciek: Acha , dzięki

Maciek: Think tylko ja mam w odpowiedziach ,że tg1 + cosπ >0.

think: Maciek, nie wiem dlaczego, tak podali w odpowiedziach, ale nie zmienię zdania ta suma jest ujemna.

think: chyba, że w treści zadania jest tg1 − cosπ , to wtedy się zgodzę

Maciek: W odpowiedziach mam coś takiego:

	π		π
1∊(		;		) i funkcja f(x)=tgx jest rosnąca w tym przedziale ,
	4		2

	π
więc tg 1 > tg		=1, cosπ = −1. Zatem tg 1 +cos π > 0.
	4

think: ehh to już rozumiem, tu nie chodzi o 1^o tylko o 1

Maciek: Możesz mi to wyjaśnić prostszym językiem

think: 1 jako liczba

π		3,14
	≈		= 0,785
4		4

π		3,14
	≈		= 1,57
2		2

think: rozumiesz czy mam próbować dalej?

think: na rysunku powinieneś zobaczyć już wszystko

Maciek:

	π
Nie rozumiem konkretnie tego : tg 1>tg		=1 ?
	4

think: popatrz na rysunek

	π
1 leży na dalej na osi niż
	4

	π
i wartość tg1 leży wyżej niż wartość tg		czyli jest większa.
	4

	π
ponieważ tg		= 1 a tg1 jest większy to znaczy że osiąga wartość większą od 1, więc jak
	4

odejmiesz od czegoś większego od 1, jedynkę to nadal zostaniesz nad kreską.

Maciek: Rozumiem teraz dziękuję Jak zawsze można na Ciebie liczyć .

think: Maciek uważaj z tym liczeniem na mnie, można się przeliczyć... Ale cieszę się, że zrozumiałeś o co biega

Maciek: Nie rozumiem jak dla mnie zawsze można na Ciebie liczyć

think: dobra na razie jak nie masz więcej pytań, to idę utopić smutki w kubku gorącej kawy z mlekiem i może dostanę nawet kawałek ciasta...

Maciek: Utopić smutki ?

think: Maciek nie jestem cyborgiem także targają mną różne uczucia, najczęściej jestem zadowolona z życia, ale siłą rzeczy jak jesteś na szczycie kiedyś musi nastać dołek.