Funkcja kwadratowa - parametr lemurek: Funkcja kwadratowa − parametr Wyznacz wartości parametru m, dla których każdy z różnych pierwiastków równania x²+x+m=0 jest większy od m. Mogę prosić o wytłumaczenie zadań tego typu, bo nie potrafię ich zrozumieć. Oczywiście na początku sprawdzamy czy Δ>0. Później, z tego co wiem, trzeba liczyć wartość funkcji dla pewnych argumentów i robić "coś" z wierzchołkiem paraboli − tego właśnie w ogóle nie rozumiem Bardzo liczę na Waszą pomoc

Godzio: W tym zadaniu ja bym nic nie kombinował z wierzchołkiem. Δ = 1 − 4m √Δ = √1 − 4m

	−1 − √1 − 4m
x1 =		> m
	2

	−1 + √1 − 4m
x2 =		> m
	2

i rozwiązać ten układ nierówności Δ > 0

−1 − √1 − 4m
	> m
2

−1 + √1 − 4m
	> m
2

Anna: Ja mam taką propozycję: Warunek 1: Δ>0 (gdyż są 2 różne pierwiastki)

	1
Δ = 1 − 4m ⇒ 1− 4m > 0 ⇒−4m > −1 ⇒ m <
	4

Warunek 2: x₁ > m x₂ > m Dodając ten układ stronami mamy: x₁ + x₂ > 2m Stosując wzór Viete'a na sumę pierwiastków:

	−b
		> 2m
	a

	1
Czyli 2m < −1 ⇒ m < −
	2

	1		1
Łącząc oba warunki, częścią wspólną jest: m ∊ (−		,		).
	2		4

lemurek: Z tego co liczę to w obu wypadkach wyjdą złe wyniki Prawidłowy to m ∊(−∞;−2)

lemurek: Ja znalazłem taki układ równań do rozwiązania, ale kompletnie nie wiem dlaczego coś takiego Δ>0 f_(m)>0 x_w<m gdzie x_w to wierzchołek paraboli

lemurek: sorry miało być x_w>0

Anna: Skąd masz ten układ, to Twój pomysł?

Anna: Wynik, który podałeś, jako prawidłowy, nie spełnia warunków zadania. Sprawdź sobie np. dla m = −1.

lemurek: ... −1 nie należy do m∊(−∞;−2) A ten układ znalazłem w podobnym zadaniu w moim zbiorze... A to co podał Godzio też wyjdzie tylko trzeba uwzględnić większy pierwiastek

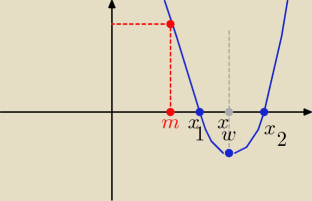
Eta: Witam Poprawna odp: m€ ( −∞, −2) Anno np: dla m=0 €( −¹₂, ¹₄) ....... nie spełni warunku zadania. Podaję rozwiązanie: by tak było, to musi być spełniony układ warunków: 1/ Δ>0 i 2/ f(m) >0 i 3/ x_w >m ( bo wierzchołek musi się znajdować na prawo od " m" 1/ Δ= 1−4m => 1−4m >0 => m <¹₄ 2/ f(m)= m²+m+m= m²+2m => m( m+2) >0 => m€ ( −∞, −2)U (0,∞) 3) x_w= ^−b_2a= −¹₂ => −¹₂ > m => m <−¹₂ wybierając część wspólną otrzymasz: odp: m€ ( −∞, −2)

think: witaj Eto, już w porządku?

Eta: Witam .......... no, powiedzmy że już w miarę

Eta: Zapomniałaś,że mam być na razem z Godziem na wielkim weselisku

think: To cieszę się, że Ci jest lepiej Ja też mam dziś ciśnienie gigant ale non stop się kręcę po domu więc nie zasnę na siedząco

think: spokojnie Godzio też jest planowany a tak poważnie, jak nie będę robiła weseliska a będę odprawiała kolejną rocznicę staropanieństwa, to jak najbardziej też jesteście mile widziani

think: i z wielkiego weseliska zrobi się np wielkie ognisko

think: dobra zmykam, całkiem możliwe, że wdrepnę tu później