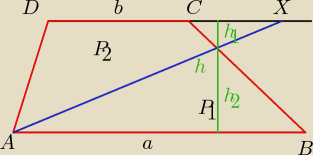
trapez Eta: Dla Godzia i Innych Zadanie z matury lat 80−tych 1/ W trapezie ADCD o podstawach IABI=a i IDCI=b na przedłużeniu DC zaznaczono punkt X tak,że prosta AX podzieliła ten trapez na dwie części o równych polach. Wyznacz długość ICXI

Eta: dla a >b

Godzio:

	a + b
Ptrapezu =		* h
	2

1		a + b
	Ptrapezu =		* h
2		4

1		ah2
	Ptrapezu =
2		2

P_trapezu = ah₂

	Pt
h2 =
	a

a		h2
	=		h1 + h2 = h => h1 = h − h2
CX		h1

a		h2
	=
CX		h − h2

a(h − h₂) = CX * h₂

	a(h − h2)
CX =
	h2

	Pt   a(h −   a
CX =
	Pt   a

	a2h − Pt * a
CX =
	Pt

	2a2 * h − (a + b)a * h
CX =
	(a+b)*h

	2a2 − a2 + ab
CX =
	a + b

	a2 + ab
CX =
	a + b

Godzio: Poczekaj jeszcze nie sprawdzaj

Eta: Będzie superr tylko wprowadź jeszcze "elegancję" zapisu

Godzio:

	2a2 − a2 − b2
CX =
	a+b

	a2 − b2
CX =
	a+b

CX = a − b

Eta: Hehe......... w/g moich obliczeń

	a−b)*a
ICXI=
	a+b

dlatego nie zauważyłam U Ciebie tego minusa w liczniku Sprawdź ....... może ja się "walnęłam"

Godzio: Chodzi o to że mam napisać że trójkąty ABS i CXS są podobne (k,k,k) gdzie S jest punktem przecięcia się prostej AX i boku AB

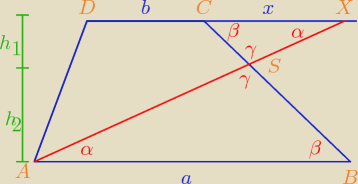Godzio: a > b, h = h₁ + h₂

	a + b
Ptrapezu =		* h
	2

1		a + b
	Ptrapezu =		* h
2		4

1		ah2
	Ptrapezu =
2		2

P_trapezu = ah₂

	Ptrapezu
h2 =
	a

Z podobieństwa ABS ~ CXS (k,k,k) mamy:

h2		a
	=		h1 = h − h2
h1		x

	a(h − h2)		Ptrapezu   a(h −   a
x =		⇒
	h2		Ptrapezu   a

	a2h − Ptrapezu * a
x =
	Ptrapezu

	2a2h − (a+b)*a*h
x =
	(a + b)* h

	2a2 − a2 − ab
x =
	a+b

	a2 − ab
x =
	a + b

	a(a − b)
x =
	a + b

Nie wiem skąd mi się wziął tam b²

Eta: Teraz jest ok A ta "elegancja" to: wyłączenie w liczniku "a" przed nawias i |CX|

Eta:

Godzio: też tak myślałem dlatego zastosowałem "x" żeby się już w to nie bawić

Eta:

AS: Oznaczenia według rysunku

h2		h1		h2*x
	=		⇒ h1 =
a		x		a

a*h2		1		a + b
	=		*		*(h1 + h2)
2		2		2

AS: dokończenie poprzedniego postu

	h2*x
2*a*h2 = (a + b)*(		+ h2) |:h2
	a

2*a² = (a + b)*(x + a)

	2*a2
x + a =
	a + b

	2*a2
x =		− a
	a + b