ciągi
TOmek : | | 3n | |
1)Dany jest ciąg (an) o wyrazie ogólnym an= |
| , n= 1,2,3,... |
| | 2 | |
c)dla jakiego x ciąg a
3, x
2−3x+9,a
5 jest ciągiem arytmetycznym
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
2)Dany jest ciag (a
n) okreslony wzorem a
n=3n+1, n≥1. Wyznacz sume trzech poczatkowych wyrazow
ciągu b
n=a
2n+1 dla n ≥1 (strasznie dziwna jak dla mnie tresc zadania)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
3)Oblicz równania
a) 1+4+7+...+(3n−2)=8n
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
4)Dany jest ciąg arytmetyczny (a
n) dla n≥1 w którym a
7=1, a
11=9
c)wyznacz takie n, dla aby suma n początkowych wyrazow ciągu a
n miałą wartość najmniejsza
(dodam ,ze a
1= −11 i r = 2 )

24 sie 13:36
Godzio:
| | 33 + 35 | |
2 * (x2 − 3x + 9) = |
| |
| | 2 | |
4x
2 − 12x + 36 = 3
3(1 + 9)
4x
2 − 12x + 36 − 10*3
3 = 0
2x
2 − 6x + 18 − 5 * 3
3 = 0
2x
2 − 6x − 117 = 0
Δ = 972
√Δ = 18
√3
| | 6 + 18√3 | | 3 + 9√3 | |
x1 = |
| = |
| |
| | 4 | | 2 | |
2.
b
n = a
2n+1 = 3(2n+1) + 1 = 6n + 4
3.
sprawdź czy dobrze przepisałeś
4.
a
n = a
1 + (n − 1)r = −11 + 2n − 2 = 2n − 13
| | −11 + 2n − 13 | | 2n2 − 24n | |
Sn = |
| * n = |
| = n2 − 12n − minimum jest w wierzchołku |
| | 2 | | 2 | |
paraboli czyli:
Odp. n = 6
24 sie 14:08
think: zad.1 c)
a
4 = x
2 − 3x + 9
z własności ciągu arytmetycznego 2a
4 = a
3 + a
5
później Δ i pierwiastki...
24 sie 14:08
TOmek : 3 dobrze na pewno , "oblicz równanie"
24 sie 14:16
Godzio:
1+4+7+...+(3n−2)=8n
W takim razie dość proste, po lewej masz sume ciągu arytmetycznego:
3n − 1 = 16
3n = 17
zazwyczaj to pisze się tego typu równania żeby były dwie niewiadome − x i n np.
1 + 4 + 7 + ... + x = 16 − i tu to juz jest inna bajka
24 sie 14:20
TOmek :
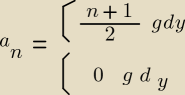
jeszcze jedno zadanko nie wiedziałem jak zrobic:
14. Nieskonczony ciąg liczbowy a
n dla n≥1 jest okreslony wzorem
| | n+1 | |
an=klamra |
| , gdy n jest nieparzyste |
| | 2 | |
=klarma
0, gdy n jest parzyste
c) oblicz sume 2008 początkowych wyrazów ciągu (a
n)
24 sie 14:24
TOmek : a) nie ma rozwiązania
tam jeszcze jest podpunkt b)3+7+11+...+(4n−1)=465 i odp jest n=15
jak nie wiecie jak roziwązac to nic

po prostu dali głupie zadanie
24 sie 14:27
Godzio:
b)
| | 3 + 4n − 1 | |
S = |
| * n = 465 |
| | 2 | |
2n
2 + n − 465 = 0
licz delte itd. pamiętaj ze n ∊N
co do 14
liczymy tylko nie parzyste czyli liczymy sumę a
2n−1
a
1 = 1
a
3 = 2
a
5 = 3
a
7 = 4
a
n = 2007
a
1 = 1
a
n = 2007
n = 1004
| | 1 + 2007 | |
Sn = |
| * 1004 = 10042 = 1008016 |
| | 2 | |
napisz czy się zgadza
24 sie 14:40
TOmek : n2 − 12n − minimum jest w wierzchołku paraboli czyli
| | 12 | |
wiem jak doszedłes do tego "n2 − 12n" ale nie wiem skąd to sie wzięło "nw= |
| "  |
| | 2 | |
24 sie 15:33
TOmek : 14) wynik = S2008=504510
24 sie 15:34
Eta:
dla
TOmka
zad. 1/ Ile liczb nalezy wstawić między liczby 62 i 440, aby otrzymać ciąg arytmetyczny,
którego suma wynosi
2008.
ponad to:
a) wyznacz róznicę tego ciągu
b) podaj wyraz ogólny
zad.2/
Trzy początkowe wyrazy malejacego ciągu arytmetycznego są pierwiastkami wielomianu:
W(x) = x
3 −3
√2 *x
2 +5x −
√2
i jednym z nich jest liczba
√2
Wyznacz:
a) pierwszy wyraz i róznicę tego ciagu
b) sumę: a
40+a
41+..... + a
80
Pozdrawiam i powodzenia

24 sie 15:40
TOmek : ok zaraz zrobie tylko wytlumaczcie mi ten post
"n2 − 12n − minimum jest w wierzchołku paraboli czyli "
24 sie 15:41
Eta:
| | −b | | 12 | |
nmin= |
| = |
| = ........  |
| | 2a | | 2 | |
24 sie 15:43
Eta:
Zatem wartość tego minimum dla n= 6 jest:
f( 6) = 62 −12*6=.........
24 sie 15:46
TOmek : a ja by było znajdz maksymalna wartość

?
24 sie 15:53
TOmek : znaczy sie najwieksza

24 sie 15:53
Eta:
Ta funkcja f(n) = n
2−12n nie ma max., bo ramiona paraboli skierowane są do góry
Chyba,że podany by był przedział , w którym może osiagać max. lokalne

24 sie 16:00
TOmek : a
1=62
2*2008=(62+a
n)*n
4016=62n+a
n*n
4016−62n=a
n*n /:n
440n=4016 − 62n
440n+62n=4016
n=8
Odp: należy wstawić 6 wyrazów
a) a
8=62+7r
440=62+7r
440−62=7r
r=54
b)a
n=62+(n−1)*54
a
n=62+54n−54
a
n=54n+8

?
24 sie 16:06
TOmek : | | −b | |
Łapie juz troche Eta, tylko zastanawiałem dlaczego podajemy do wyniku p=x ( |
| ) myślałem |
| | 2a | |
,ze trzeba podac y

24 sie 16:08
TOmek : jak ja to zadanie zrobiłem dobrze to dla mnie naprawde ogromny sukces xD ale pewnie gdzie sie
rąbnąłem

24 sie 16:12
Eta:

utrudniasz sobie życie:
502n= 2008 => n= 8
odp: należy wstawić 6 wyrazów
r=54
a
n= 54n+8 −−− ok:
24 sie 16:14
Eta:
Jeżeli masz w pytaniu do zadania:
" podaj dla jakiego "x" kwadratowa funkcja f(x) osiaga max."
a jezeli masz podac
wartość tego max.
to wartość = f( x
max)=........
24 sie 16:17
TOmek : ok dziekuje

zapamiętam, zrobiłem dobrze zadnko \o/ xD
aha miałem jeszcze takie pytanie do tego pierwszego
| | 4016 | |
an= |
| − 62 można nazwać wzorem do obliczania którym wyrazem jest a n tak  |
| | 2 | |
24 sie 16:19
TOmek : 2)
(x
3 −3√2 *x
2 +5x −√2):(x−
√2) //(x−(+
√2)
√2
1 | −3√2 | 5 | √2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
1 | −2
√2 | 1 |
2√2 R
√2−3
√2=−2
√2
−2
√2*
√2+5=−4+5=1
√2+
√2=2
√2
(x
3 −3√2 *x
2 +5x −√2)=(x−
√2)(x
2−2
√2x+1)+2
√2
Δ=(−2
√2)
2−4*1*1
Δ=8−4=4
√Δ=2
| | 2√2+2 | | 2(√2+1) | |
x1= |
| = |
| =√2+1 |
| | 2 | | 2 | |
| | 2√2−2 | | 2(√2−1) | |
x2= |
| = |
| =√2−1 |
| | 2 | | 2 | |
√2−1,
√2,
√2+1
a
2=
√2−1+r
√2−
√2+1+r
r=1
a
1=
√2−1
24 sie 16:30
TOmek : żle tutaj ciąg jest malejący więc
√2+1, √2 , √2−1
r= −1
24 sie 16:31
Eta:
No nie

...... to bzdura , sprawdź sam i się o tym przekonasz ( wykonaj obliczenia) i
wyjdzie "kicha"

2S
n= ( a
1+a
n)*n
| | 4016 | | 4016 | |
zatem: n= |
| = |
| = 8 , czyli ok  |
| | 62+440 | | 502 | |
24 sie 16:31
TOmek : "utrudniasz sobie życie: " −> ten post ⇔ naprawdę nie wpadł bym nigdy na takie
rozwiązanie

heh, ile ja jeszcze nie wiem

24 sie 16:32
TOmek : to bzdura czy prawda

xD
24 sie 16:33
TOmek : jak będzie dobrze 2 to zrobie b) sumę: a40+a41+..... + a80
24 sie 16:34
Eta:
zad.1/ ok

r= −1 a
1=
√2+1 ( bo ciąg jest malejący)

za schemat Hornera

24 sie 16:35
TOmek : "No nie ...... to bzdura , sprawdź sam i się o tym przekonasz ( wykonaj obliczenia) i wyjdzie
"kicha" emotka"
dziwne masz metody nauczania xD
Napisz ,ze dobrze pisze a nie, dajesz mi metaforyczne mysli, których nie rozumiem

robie b
24 sie 16:39
Eta:
No cóż , skoro "mam dziwne metody nauczania"

To zrezygnuj z mojej pomocy

Niw widzę nic dziwnego? w tm,że:
otrzymasz: 440= 2008 − 62 −−−−− a to nie jest prawdą !
Dlatego napisałam Ci,że to "bzfura" !

powodzenia !
24 sie 16:46
TOmek : b) sumę: a
40+a
41+..... + a
80
a
1= √2+1
r= −1
a
n=√2+1+(n−1)*(−1)
a
n=√2+1−n+1
a
n= −n+
√2+2
a
40= −38+
√2
a
80= − 80 +
√2+2
a
80= − 78 +
√2
czyli można powiedzieć ,ze mamy ciąg nowy ciąg gdzie
a
1= −38+
√2
a
41= − 78 +
√2
| | −38+√2 − 78 +√2 | |
S41= |
| *41 |
| | 2 | |
S
41=(−116+2
√2)*20,5
S
41= − 2378 + 41
√2
na bank coś spieprzyłem

24 sie 16:51
TOmek : nie obrażaj sie to był żarcik

po prostu nie zrozumiałem twojego postu, moja wina
24 sie 16:52
TOmek : a tamtym poście źle napisałem, jeszcze raz
czy
| | 4016 | |
an= |
| − 62 można nazwać wzorem do obliczania którym wyrazem jest a n |
| | n | |
dlatego chyba zaszło te nieporozumienie

bo ja myślałem ,ze tam zamiast 2 jest n xD. Moj big
błąd
24 sie 16:56
TOmek : Eta


możemy ciągnąc dalej temat

bo nie wiem czy dobrze zrobiłem b) czy
powyzszy post po poprawce jest trafny nic nie wiem

24 sie 17:08
Godzio:
Wynik się zgadza.
24 sie 17:22

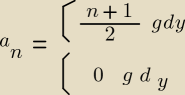 jeszcze jedno zadanko nie wiedziałem jak zrobic:
14. Nieskonczony ciąg liczbowy an dla n≥1 jest okreslony wzorem
jeszcze jedno zadanko nie wiedziałem jak zrobic:
14. Nieskonczony ciąg liczbowy an dla n≥1 jest okreslony wzorem
 po prostu dali głupie zadanie
po prostu dali głupie zadanie

 zad. 1/ Ile liczb nalezy wstawić między liczby 62 i 440, aby otrzymać ciąg arytmetyczny,
którego suma wynosi 2008.
ponad to:
a) wyznacz róznicę tego ciągu
b) podaj wyraz ogólny
zad.2/
Trzy początkowe wyrazy malejacego ciągu arytmetycznego są pierwiastkami wielomianu:
W(x) = x3 −3√2 *x2 +5x −√2
i jednym z nich jest liczba √2
Wyznacz:
a) pierwszy wyraz i róznicę tego ciagu
b) sumę: a40+a41+..... + a80
Pozdrawiam i powodzenia
zad. 1/ Ile liczb nalezy wstawić między liczby 62 i 440, aby otrzymać ciąg arytmetyczny,
którego suma wynosi 2008.
ponad to:
a) wyznacz róznicę tego ciągu
b) podaj wyraz ogólny
zad.2/
Trzy początkowe wyrazy malejacego ciągu arytmetycznego są pierwiastkami wielomianu:
W(x) = x3 −3√2 *x2 +5x −√2
i jednym z nich jest liczba √2
Wyznacz:
a) pierwszy wyraz i róznicę tego ciagu
b) sumę: a40+a41+..... + a80
Pozdrawiam i powodzenia 

 ?
?


 ?
?


 utrudniasz sobie życie:
utrudniasz sobie życie:
 zapamiętam, zrobiłem dobrze zadnko \o/ xD
aha miałem jeszcze takie pytanie do tego pierwszego
zapamiętam, zrobiłem dobrze zadnko \o/ xD
aha miałem jeszcze takie pytanie do tego pierwszego

 ...... to bzdura , sprawdź sam i się o tym przekonasz ( wykonaj obliczenia) i
wyjdzie "kicha"
...... to bzdura , sprawdź sam i się o tym przekonasz ( wykonaj obliczenia) i
wyjdzie "kicha" 

 heh, ile ja jeszcze nie wiem
heh, ile ja jeszcze nie wiem 
 xD
xD
 r= −1 a1= √2+1 ( bo ciąg jest malejący)
r= −1 a1= √2+1 ( bo ciąg jest malejący)
 za schemat Hornera
za schemat Hornera 
 robie b
robie b
 To zrezygnuj z mojej pomocy
To zrezygnuj z mojej pomocy  Niw widzę nic dziwnego? w tm,że:
Niw widzę nic dziwnego? w tm,że:
 powodzenia !
powodzenia !

 po prostu nie zrozumiałem twojego postu, moja wina
po prostu nie zrozumiałem twojego postu, moja wina

 bo ja myślałem ,ze tam zamiast 2 jest n xD. Moj big
błąd
bo ja myślałem ,ze tam zamiast 2 jest n xD. Moj big
błąd

 możemy ciągnąc dalej temat
możemy ciągnąc dalej temat bo nie wiem czy dobrze zrobiłem b) czy
powyzszy post po poprawce jest trafny nic nie wiem
bo nie wiem czy dobrze zrobiłem b) czy
powyzszy post po poprawce jest trafny nic nie wiem 