ciągi TOmek: 1)Dany jest ciąg (b_n) okreslony wzorem b_n=n²−7n−18 n∊N₊ ile wryazów ciągu (b_n) jest liczbami ujemnymi? no to robie n²−7n−18<0 √Δ=11

	7+11
x1=		=9
	2

	7−11
x2=		= −2
	2

Czyli jest 9 liczb ujemnych a w odp jest 8 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	n+2
2)Dany jest ciąg (an), gdzie Sn=		dla n=1,2,3...Wyznacz wszystkie wyrazy tego
	3n+1

	1
ciągu wiekszę od
	2

n+2		1
	>
3n+1		2

n+2		1
	−		>0
3n+1		2

2n+4		3n+1
	−		>0
2*(3n+1)		2*(3n+1)

2n+4−3n−1
	>0
2*(3n+1)

(−n+3)*(6n+2)>0 −6n²−2n+18n+6>0 −6n²+16n+6>0 √Δ=20

	−16+20		4		1
x1=		=		=−
	−12		−12		3

	−16−20		−36
x2=		=
	−12		12

	3		4
a w odp jest : a1=		a2=
	4		7

Godzio: 1. n ∊ N₊ ! Odpowiedź to: 8,7,6,5,4,3,2,1

Godzio:

	1
2. Ty policzyłeś kiedy suma jest większa od		a nie an
	2

musisz policzyć coś takiego, tak jak we wcześniejszym zadaniu ktore dawałeś S_n − S_n−1 = a_n

	1
an >
	2

TOmek: ok juz wiem w czym tkwią moja głupie błędny danke

Eta: I moja nauka "poszła w las" Pozdrawiam

TOmek: w tym 2 zadanku nie S_n tylko a_n to po korekcie dlacego mam źle?

Godzio:

	n + 2
czyli an =		?
	3n + 1

Godzio:

n+2		1
	>		/ * 2(3n+1) −− możemy tak zrobić bo 3n + 1 > 0 dla n ∊ N+
3n+1		2

2n + 4 > 3n + 1 n < 3 czyli są tylko 2 takie wyrazy a₁ i a₂ w poleceniu jest że mamy je wyznaczyć więc:

	1 + 2		3
a1 =		=
	3 * 1 + 1		4

	2 + 2		4
a2 =		=
	3 * 2 + 1		7

TOmek: to gdzie ja kurna błąd zrobiłem w moim powyzszym rozwiązaniu

Godzio: zamieniłeś iloraz na iloczyn niepotrzebnie

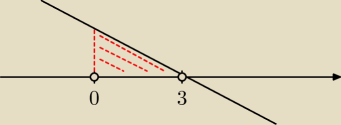
Godzio: ale można tak w sumie też bo:

	1
n1 = −		− odpada bo n ∊ N
	3

	−36
n2 =		= 3
	−12

czyli rysuje prostą przechodzącą przez 3 zaczynając od dołu bo jest −6n² i sprawdzam gdzie jest większa od zera czyli odp: n ∊ {1,2} i teraz liczysz wartości dla n = 1 i n = 2

TOmek: przeciez tak sie to rowiązauje (nauczyłem sie tego z działu "funkcja wymierna")

Godzio: no tak tak ale

	x + 2
tutaj:		> 0 ⇔ (x + 2)(x − 1) > 0 − nie wiemy czy x − 1 jest dodatnie czy ujemne
	x − 1

dlatego tak jest ale w tym przypadku wiemy że mianownik jest dodatni to nie musimy tak robić

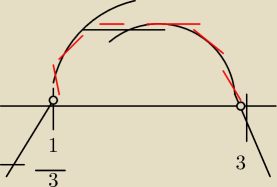
TOmek: a∊1,2,3 takze n∊(1,2) czaje

TOmek: nie wiemy czy x − 1 jest dodatnie czy ujemne troche mi zagmatwałes tym ostatnim postem, moze bardziej dokładnie rozwinąć swoja mysl, chodzi mi o tę początkową cześć zdania bo to ,ze "ale w tym przypadku wiemy że mianownik jest dodatni to nie musimy tak robić " to rozumiem

	n+2		1
to jak jesli mam taki przykład		>		i nie jest to nigdzie zapisane ,ze n∊N to
	3n+2		2

nie mogę rozwiązywac metodą z "funkcji wymiernej" ?

Godzio: w ciągach n jest zawsze dodatnie więc jeśli widać że mianownik jest dodatni to nie mozna sie go pozbyc

jeremi: "widać że mianownik jest dodatni" 3n+1 dla N₊ to mozna sie go pozbyc* xD a nie nie mozna sorki ,ze jestem strasznie natrętny ale ja chce znac odp na wszystkie pytania inaczej nie zasne xD

jeremi: jeremi=TOmek xD

Godzio: no chodziło że można

n + 3
	> 0
n + 5

n + 3 > 0 n > − 3 ⇒ N₊

4n + 2
	< 0
n + 1

4n + 2 < 0 n < −U{1}{2] n ∊ ∅

TOmek : \o/ pierwszy raz poprawiłem Godzia −> nic dziwnego bo go męcze od paru godzin xD wnioski 1)

	n+3
		>0 czyli jak wiemy ze mianownik jest dodatki bo np w tresci jest ,ze n∊N+
	n+5

(albo rozwiązaujemy zadanko z ciągów) i po podsawieniu do n + 5 liczby (1,2,3,4...zawsze wychodzi dodatni to mozemy usunac mianownik 2) jednak jak rozwiazaujemy jakies inne zadanko (nie z ciagów) musimy postepowac jak w "funkcji wymiernej"

n+3
	>0
n+5

(n+3)*(n+5)>0 3) a jak wiemy ,ze mianownik jest ujemny to takze mozemy usunac mianownik ta

Godzio: tak ale ze zmianą znaku

TOmek : no rozumiem