wartość bezwzględna alisior: oblicz: 14=|2x+6|+|2−x| bardzo proszę o wytłumaczenie krok po kroku jak to wykonać.

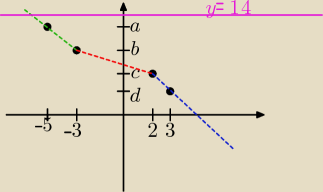
think: narysuj wykres: f(x) = |2x + 6| + |2 − x| policz: f(−5) = ....a f(−3) = ....b f(2) = .....c f(3) = .....d narysuj łamaną łącząc kolejno te pukty, jak na rysunku, te punkty mogą wyjść zupełnie inne niż narysowałam, ale to będzie dokładnie wykres tej funkcji z tymi funktami które Ci wyjdą. Na końcu musisz odczytać z wykresu dla jakiego x wykres tej funkcji przecina prostą y = 14. /* teraz wyjaśniam dlaczego wybrałam punkty −5,−3,2,3; −3 i 2 to są punkty dla których zeruje się jedna albo druga wartość bezwzględna, −5 jest liczbą mniejszą od −3 a liczba 3 jest większa od 2, dzięki tym dwóm punktom po bokach mozna narysować wykres wartości bezwzględnej, polecam

TOmek: szukam msc. zerowych 2x+6=0 2x=−6 x=−3 2−x=0 −x=−2 x=2 Znajduje przedziały (−∞,−3) <−3,2) (2,∞) 1) dla x ∊(−∞,−3) (czyli podstawiamy np: −4,−5,−6) 2x+6 < x ⇔ −(2x+6) 2−x > x ⇔ 2−x −−−−−−−−−−−−−−−−−−−−−−−−− 14=|2x+6|+|2−x| 14=−2x−6+2−x 14+6−2=−x−2x 18=−3x −3x=18 x= −6 x ∊(−∞,−3) także −6 zgadza się 2) dla <−3,2) 2x+6 ≥ x ⇔ 2x+6 2−x > x ⇔ 2−x −−−−−−−−−−−−−−−−−−−−−−−−−−−−− 14=|2x+6|+|2−x| 14=2x+6+2−x 14−6−2=2x−x x=6 dla <−3,2) nie nalezy 3) dla (2,∞) 2x+6 > x ⇔ 2x+6 2−x < x ⇔ −(2−x)⇔−2+x 14= 2x+6−2+x 14=2x+6−2+x 14−6+2=2x+x 10=3x x=3,(3) czyli należy do przedziału (2,∞) Odp: Liczby 3,(3) i −6 są rozwiązaniami rownania 14=|2x+6|+|2−x| think prosze sprawdź

Godzio: Nie jestem think ale powiem tak: jest ok, tyle że ten zapis typu 2x + 6 ≥ x ⇔ 2x + 6 jest nie poprawny jeśli już chcesz tak pisać to dla <−3,2) 2x + 6 ≥ 0 ⇒ |2x + 6| = 2x + 6

TOmek: będę pamiętał

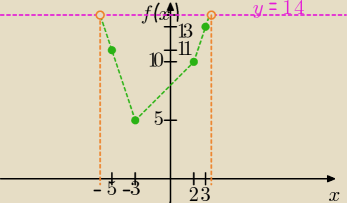
think: nie było mnie trochę, ale nieoceniony Godzio zawsze czuwa TOmek ja proponowałam rozwiązać to graficznie, bynajmniej nie zrobiłeś tego metodą zaproponowaną przeze mnie a szkoda. f(x) = |2x + 6| + |2 − x| f(−5) = |−10 + 6| + | 2 + 5| = 11 f(−3) = | −6 + 6| + |2 + 3| = 5 f(2) = |4 + 6| + |2 − 2| = 10 f(3) = |6 + 6| + |2 − 3| = 13

	1
Rozwiązanie to: −6 i 3
	3

TOmek : takie jeszcze pytanko do think jak robie zadania takiego typu, to przy ustalaniu przedziałow (−∞,−3) <−3,2) (2,∞) lewa stronka zawsze musi być "<" domknięta(wyjątek nieskonczonosc) ta? i to nie ma znaczenie czy 14>|2x+6|+|2−x| 14≤|2x+6|+|2−x| przedziały do liczenia moją metodą będą zawsze takie same(biorąc pod uwage powyzsze przykłady)?/ ta

think: TOmek, spokojnie możesz pisać (−∞,−3> <−3,2> <2,∞) w każdym razie gdy rozwiązywałam zadania w ten sposób zanim zaczęłam to robić graficznie.

think: sorki, że tak długo musiałeś czekać na opowiedź, ale jestem w pracy i akurat trochę luda się zwaliło