ciągi
TOmek:

1) dany jest ciąg arytmetyczny (a
n) o wyrazie pierwszym a
q=5m−1 i różnicy r=9−m
2
b)wyznacz, dla jakich wartosci parametru m ciąg (a
n) jest rosnący.
kurna i mi nie wychodzi
r>0 −>ciąg jest rosnący
9−m
2>0
−m
2>−9
m
2<9
m<3
lub
m<−3
a w odp jest m∊(−3,3)





2)Dany jest ciąg arytmetyczny (a
n) gdzie n≥1. Wiadomo ,ze dla kazdego n≥1 suma n początkowych
wyrazów S
n=a
1+a
2+...+a
n
a)wyznacz wzór na n−ty wyraz ciągu
(wiem jak to robić ale mi zły wynik wychodzi

)
22 sie 19:35
Godzio:
zad. 1
m2 < 9 /√
|m| < 3
m < 3 i m > − 3
22 sie 19:56
Godzio: zad 2.
S
n = a
1 + a
2 + ... + a
n
S
n−1 = a
1 + a
2 + ... + a
n−1
| | a1 + a1 + (n−1)r | | a1 + a1 + (n−2)r | |
an = Sn − Sn−1 = |
| *n − |
| * (n−1) = |
| | 2 | | 2 | |
| | 2a1 + (n−1)r | | 2a1 + (n−2)r | | 2a1 + (n−2)r | |
= |
| *n − |
| *n + |
| = |
| | 2 | | 2 | | 2 | |
| | 2a1n + rn2 − rn − 2a1n − n2r + 2rn + 2a1 + nr − 2r | |
= |
| = |
| | 2 | |
| | 2rn + 2a1 − 2r | |
= |
| = = a1 + rn − r = a1 (n − 1)r |
| | 2 | |
O takie coś chodziło ?
22 sie 20:02
TOmek: wybacz, Godzio przez mój błąd zabrałem Ci niepotrzebnie troche czasu

2)Dany jest ciąg arytmetyczny (a
n) gdzie n≥1. Wiadomo ,ze dla kazdego n≥1 suma n początkowych
wyrazów Sn=a
1+a
2+...+a
n, wyraża sie wzorem S
n= −n
2+13n
a)wyznacz wzór na n−ty wyraz ciągu
wybacz ...
22 sie 21:20
TOmek:
m
2<3
|m| < 3
m < 3
lub
m > − 3
dlaczego tak

(albo pierwszy raz widzę takie coś albo dzisiaj jestem naprawdę nie w pełni
sprawny

ja myślałem ,ze to się robi w nastepujacy sposob
m
2<9
m<3
lub
m<−3
22 sie 21:24
Godzio:
√a2 = |a|
m2 < 9
|m| < 3
m ∊ (−3,3)
m2 > 9
|m| > 3
m ∊ (−∞,−3)∪(3,∞)
22 sie 21:29
TOmek: dziwi mnie najbardziej zmiana znaku
|m| < 3
m < 3
m > − 3
z def. wart. bezwzględnej |a|= −a lub |a|= a więc dlaczego jest zmiana znaku?
22 sie 21:33
Godzio: z definicji wartości bezwzględnej
|x| = a a ∊ R+
x = a v x = −a
|x| < a
x < a ∧ x > −a
|x| > a
x > a ∨ x < − a
22 sie 21:35
TOmek: dziekuje pięknie za wytłumaczenie, mógłbys jeszcze zadanko 2 zrobić?
22 sie 21:38
Godzio:
nie wiem za bardzo o co w nim chodzi

22 sie 21:40
TOmek: 2)Dany jest ciąg arytmetyczny (an) gdzie n≥1. Wiadomo ,ze dla kazdego n≥1 suma n początkowych
wyrazów Sn=a1+a2+...+an, wyraża sie wzorem Sn= −n2+13n a)wyznacz wzór na n−ty wyraz ciągu
−−−−−−−−−−−−−−−−−−−−
zeby wyznaczyc wzór nan−ty wyraz musze miec a1 i r
S1= 1+13*1=14
a1=14
S2=4+26=30
a1+a2=30
a2=16
a2=14+r
16−14=r
r=2
an=a1+(n−1)*r
an=14+(n−1)*2
an=14+2n−2
an=2n+12
a w odp jest an=−2n+14
22 sie 21:49
Eta:

zad.2/ S
n − S
n−1=
an
22 sie 21:54
Eta:
taki właśnie wynik otrzymasz:
an= −2n+14

22 sie 21:57
TOmek: S
2 − S
2−1= a
2
S
2 − S
1= a
2
30 − 14 = a
2
a
2=16
no i nie wyjdzie
wybaczcie ,pewnie robię jakiś głupi błąd, ale dopiero od 4 dni wiem ,ze istnieją ciągi

22 sie 22:05
Eta:
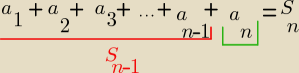
S
n −
Sn−1=
an
22 sie 22:05
Eta:
No to dokończmy

a
n= −n
2+13n−[−(n−1)
2 +13(n−1)]= −n
2+13n +(n
2−2n+1 −13n +13)= −2n +14
22 sie 22:08
TOmek: mogłabyś to w jakimś innym zapisie to przedstawić

22 sie 22:10
Eta:
Zapamiętaj tę zależność

Jeżeli ciąg jest dany przez sumę
to:
an =
Sn−Sn−1
22 sie 22:11
TOmek: an = Sn−Sn−1
gdzie:
Sn=−n2+13n
Sn−1=[−(n−1)2 +13(n−1)] −> skąd Ty to wzięłas?
22 sie 22:14
Eta:
W jakim innym?
Podałam Ci wszystko "na tacy"( włacznie z rysunkiem)
chyba widzisz,że jeżeli od sumy S
n
odejmiesz sumę (n−1) początkowych wyrazów,to:
co Ci zostaje? ......... no wyraz ostatni, czyli
an
i to wszystko

22 sie 22:16
TOmek: Sn−1= to suma o 1 mniejsza o sumy n−tej
22 sie 22:17
TOmek: znaczy sie o jedno "a"
S
n−1=[−(n−1)2 +13(n−1)] −> skąd Ty to wzięłas? Tylko tego nie wiem

22 sie 22:19
Eta:
za n w sumie S
n podstawiasz ( n−1)
bo liczysz sumę S
n−1
zatem S
n−1= −(n−1)
2 +13( n−1)= −( n
2−2n+1) +13n −13= −n
2 +2n −1+13n −13=
S
n−1= −n
2 +15n −14
teraz tylko odjąć
a
n=S
n− S
n−1= −n
2 +13n +n
2 −15n +14= −2n +14

22 sie 22:20
TOmek: dziekuje pięknie wszystko pięknie mi wytłumaczyłas, niech Bóg Ci to wynagrodzi w dzieciach,
pozdawiam dobranoc!

22 sie 22:22
TOmek: Godziowi także dziekuje za dzisiejsze posty

22 sie 22:22
Eta:
Hehe....... w dzieciach? ( to już nie dla mnie


Chyba,że we wnukach

( mam już dwoje wnusiów

Dobranoc

22 sie 22:25
TOmek: Mam jedno pytanko
Napisze wszystko o co chodzi w jednym poscie by nie trzeba było szukac: więc tak:
2)Dany jest ciąg arytmetyczny (a
n) gdzie n≥1. Wiadomo ,ze dla kazdego n≥1 suma n początkowych
wyrazów Sn=a
1+a
2+...+a
n, wyraża sie wzorem S
n= −n
2+13n
a)wyznacz wzór na n−ty wyraz ciągu
S
1= 1+13*1=14
a1=14
S
2=4+26=30
a
1+a2=30
a2=16
a2=14+r
r=2
tu się wszystko chyba zgadza
−−−−−−−−−−−−−−−−−−−−−−−
Eta obliczyła to w nastepujący sposob:
a
n= −n
2+13n−[−(n−1)
2 +13(n−1)]= −n
2+13n +(n
2−2n+1 −13n +13)=
−2n +14 (taki jest wynik
w odpowiedziach
ale można to zrobic przeciez na 2 sposób
r=2
a
1=14
an=a1+(n−1)*r
a
n=14+(n−1)*2
a
n=14+2n−2
a
n=2n+12
To przeciez tu tez powinien wyjść dobry wynik prawda

?
Noo chyba ,ze 2n+12 = −2n +14 ale tak nie jest ....
23 sie 13:01
TOmek: czy to może jest takie specyficzne zadanie

23 sie 13:17
TOmek: 
23 sie 13:54
Godzio: S1 = −1 + 13 = 12
S2 = −4 + 26 = 22
12 + a2 = 22
a2 = 10
r = −2
an = a1 + (n−1) = 12 − 2n + 2 = −2n + 14
Staraj się dokładnie robić zadania
23 sie 14:28
TOmek: −n2= − (−1)2= −1
dziekuje pięknie
23 sie 15:46
TOmek: Wracając do tego
√a2 = |a|
m2 < 9
|m| < 3
m ∊ (−3,3)
−−−−−−−−−−−−−−−−−−−−−−
jakby było
m2<3 / √
√m2<3 / widzimy wzór √a2=|a|
|m|<√3
m∊(−√3,√3)
dobrze?
23 sie 17:47
TOmek: i jeszcze:
m
2 ≤ 3
m∊<−√3,√3>
ta

23 sie 17:48
Godzio:
dokładnie tak
23 sie 17:51
 1) dany jest ciąg arytmetyczny (an) o wyrazie pierwszym aq=5m−1 i różnicy r=9−m2
b)wyznacz, dla jakich wartosci parametru m ciąg (an) jest rosnący.
kurna i mi nie wychodzi
r>0 −>ciąg jest rosnący
9−m2>0
−m2>−9
m2<9
m<3
lub
m<−3
a w odp jest m∊(−3,3)
1) dany jest ciąg arytmetyczny (an) o wyrazie pierwszym aq=5m−1 i różnicy r=9−m2
b)wyznacz, dla jakich wartosci parametru m ciąg (an) jest rosnący.
kurna i mi nie wychodzi
r>0 −>ciąg jest rosnący
9−m2>0
−m2>−9
m2<9
m<3
lub
m<−3
a w odp jest m∊(−3,3) 



 2)Dany jest ciąg arytmetyczny (an) gdzie n≥1. Wiadomo ,ze dla kazdego n≥1 suma n początkowych
wyrazów Sn=a1+a2+...+an
a)wyznacz wzór na n−ty wyraz ciągu
(wiem jak to robić ale mi zły wynik wychodzi
2)Dany jest ciąg arytmetyczny (an) gdzie n≥1. Wiadomo ,ze dla kazdego n≥1 suma n początkowych
wyrazów Sn=a1+a2+...+an
a)wyznacz wzór na n−ty wyraz ciągu
(wiem jak to robić ale mi zły wynik wychodzi )
)
 2)Dany jest ciąg arytmetyczny (an) gdzie n≥1. Wiadomo ,ze dla kazdego n≥1 suma n początkowych
wyrazów Sn=a1+a2+...+an, wyraża sie wzorem Sn= −n2+13n
a)wyznacz wzór na n−ty wyraz ciągu
wybacz ...
2)Dany jest ciąg arytmetyczny (an) gdzie n≥1. Wiadomo ,ze dla kazdego n≥1 suma n początkowych
wyrazów Sn=a1+a2+...+an, wyraża sie wzorem Sn= −n2+13n
a)wyznacz wzór na n−ty wyraz ciągu
wybacz ...
 (albo pierwszy raz widzę takie coś albo dzisiaj jestem naprawdę nie w pełni
sprawny
(albo pierwszy raz widzę takie coś albo dzisiaj jestem naprawdę nie w pełni
sprawny  ja myślałem ,ze to się robi w nastepujacy sposob
m2<9
m<3
lub
m<−3
ja myślałem ,ze to się robi w nastepujacy sposob
m2<9
m<3
lub
m<−3

 zad.2/ Sn − Sn−1= an
zad.2/ Sn − Sn−1= an


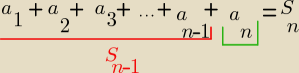 Sn − Sn−1= an
Sn − Sn−1= an
 an= −n2+13n−[−(n−1)2 +13(n−1)]= −n2+13n +(n2−2n+1 −13n +13)= −2n +14
an= −n2+13n−[−(n−1)2 +13(n−1)]= −n2+13n +(n2−2n+1 −13n +13)= −2n +14

 Jeżeli ciąg jest dany przez sumę
to: an = Sn−Sn−1
Jeżeli ciąg jest dany przez sumę
to: an = Sn−Sn−1






 Chyba,że we wnukach
Chyba,że we wnukach  ( mam już dwoje wnusiów
( mam już dwoje wnusiów  Dobranoc
Dobranoc
 ?
Noo chyba ,ze 2n+12 = −2n +14 ale tak nie jest ....
?
Noo chyba ,ze 2n+12 = −2n +14 ale tak nie jest ....


