trygonometria -> prośba TOmek: Jak ktoś ma czas to poprosze parę zadanek na poziomie matury roz. z trygonometrii(4,5 zadanek). Powrórzyłem sobie materiał i potrzebuje takiego zwięczenia pozdarwiam Godzia

yyy: 1. Sprawdź czy dana równość jest tożsamościa trygonometryczną

	4 cos2x
a.		=sin22x
	ctg2x−tg2x

	1+sin4x		1+tg2x
b.		=
	cos4x		1−tg2x

TOmek: za cholere nie mogę zrobić a) kosmiczne ułamki ... ide obsawic lige europejska do millenium moze tam coś mi lepiej wyjdzie !

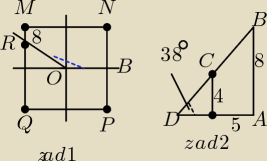
Mateusz: Moze ja cos dorzuce zad 1 Punkt O jest środkiem symetrii kwadratu MNOPQ wiedząc ze |RO| = 8 i α(niebieska przerywana linia) = 145^o oblicz pole pięciokąta ORMNBQ zad 2 który z odcinków jest dłuższy BC czy CD?(na rysunku zaznaczyłem kąt 38⁰) zad 3 Znajdz wszystkie rozwiązania równania 11*sin(0,16x−1,66)+7,21=18 zad 4 Sprawdz czy zachodzi równość:

	π		3
tg(		−α)*ctg(		π−α)=1
	2		2

Mam nadzieje ze nie za łatwe

yyy: to ja jeszcze 2.wyznacz dziedzinę i zbiór wartości funkcji

	1−sin4x−cos4x
f(x)=
	1−cos2x−sin6x

yyy: coś z równań

4cosx−sin2x
	=4cos2x
cosx

yyy: co do podpunktu a z zadania 1.

	4(cos2x−sin2x
L=		=U{4(cos2x−sin2x)
	cos2xsin2x−sin2xcos2x

}{^{cos4x−sin4x}_sin²xcos²x=U{4(cos²x−sin²x)sin²xcos²x}{cos⁴x−sin^ 4x}=U4(cos²x−sin²x)sin²xcos²x}{(cos²x−sin²x)(cos²x+sin²x)}=U{4sin²x cos²x}{cos²x+sin²x}=4sin²xcos²x=sin²2x L=P

yyy: ehh. coś z zapisem nie wyszło spróbuję jeszcze raz

TOmek:

	1−sin4x−cos4x
f(x)=
	1−cos2x−sin6x

sin²x−sin⁶x≠ 0 sin²x(1−sin⁴x) ≠ 0 x₁=0 ⇔ x=kπ

	π
x2=1 ⇔ x=		+ 2kπ
	2

	−π
x3= −1 ⇔ x=		+2kπ
	2

	π		−π
D=R \ x ∊{kπ,		+ 2kπ,		+2kπ}
	2		2

1−sin⁴=0 −sin⁴=−1 sin⁴=1 sin=1 sin=−1 dobrze chociaz dziedzinę wyznczyłem?

Godzio: Dziedzina ok tylko x ≠ ... a nie x =

TOmek:

4cosx− sin2x
	=4cos2x
cosx

cosx≠0

	π
x∊		+kπ k∊C
	2

	π
D=R \ {		+kπ}
	2

4cosx− sin2x
	=4cos2x / * cos
cosx

4cosx− sin2x=4cos³x ***sin2x=2sin*cos 4cosx−2sin*cos−4cos³x=0 /:2 2cosx−sin*cos−2cos³x=0 dobrze na razie

TOmek: jest Godzio \o/

Godzio: zdaję się że tak chodź trochę inaczej bym to zaczął

TOmek: no i co teraz (zrobiłem już tak więc będe sie do koncza meczyl) 2cosx−sin*cos−2cos³x=0

Godzio: podziel na cosx i dalej musisz sam coś zauważyć

TOmek: 2cosx−sin*cos−2cos³x=0 / cos

2cosx		sincos		2cos3x
	−		−		=0
cosx		cos		cos

2cosx		sincos		2cos3x
	−		−		=0
cosx		cos		cos

2*0 − sin − 2cos² = 0 −sin − 2cos² = 0 dobrze

Godzio:

cosx
	= ?
cosx

TOmek: 1 z/w obiad

Godzio: Mateusz w tym pięciokącie wyszło ≈ 77,52 ?

TOmek: 2 − sin − 2cos²=0 2−sin − 2*(1−sin²)=0 2−sin−2+2sin²=0 sin²−2sin=0 sin(2sin−1)=0 sin₁=0 x∊kπ k∊C −−−−−−−−−−−−−−−−−−−−− 2sin−1=0 2sin=−1

	1		π		5π
sin= −		x∊		+2kπ v		+2kπ
	2		6		6

	π		5π
Odp: x∊{kπ,		+2kπ,		+2kπ}
	6		6

TOmek: hmm?

Godzio:

	1
sinx = −
	2

	π		7π
x = −		+ 2kπ v x =		+ 2kπ
	6		6

Godzio: Ale jeszcze wróć do tamtego zadania z dziedziną i zbiorem wartości − przekształć to wyrażenie do najprostszej postaci i może wtedy zobaczysz zbiór wartości

TOmek: musiałem sie zaguić

1		π
	to
2		6

wyobrazając sobie ten wykres https://matematykaszkolna.pl/strona/1579.html wychodzi:

	π		6π		π		5π
−π+		+2kπ = −		+		+2kπ= −		+2kπ tak tez moze byc
	6		6		6		6

	π
−		+2kπ
	6

Godzio: Jeśli o to chodzi:

	π		5π
x = −		+ 2kπ v x =−		+ 2kπ to tak
	6		6

Mateusz: Godzio albo ty masz bąd albo ja mi wyszło P≈70,85

Godzio: Sprawdzę jeszcze raz

Godzio: jak 2 razy liczyłem to mi wyszły 2 inne wyniki z tym że robiłem na 2 różne sposoby to już nie wiem bo teraz mi wyszło 92 a wcześniej 98

Godzio: 1.

	1		1		1
P1 =		* a *		a =		a2
	2		2		4

	1		1		1		1
P2 =		*		a *		a =		a2
	2		2		2		8

	1		1
P3 =		*		a * 8 * sin35 = 2asin35
	2		2

	1
cos35 =		a / 8
	2

a ≈ 13,11 P = a² − P₁ − P₂ − P₃ = 92,38 i błędu żadnego nie widzę 2. a ≈ 13,11

	1   a − x 2
sin35 =
	8

	1
x =		a − 4,59
	2

	1		1		1		1
P1 =		*		a *		a =		a2
	2		2		2		8

	1		2
P2 =		a2 =		a2
	4		8

	a − 4,59		1		a2 − 4,59a		2a2 − 9,18a
P3 =		*		a =		=
	2		2		4		8

	5a2 − 9,18a
P = P1 + P2 + P3 =		≈ 92,35
	8

I z tego wychodzi że chyba dobrze