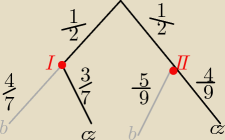
jak rązwiązać i małe wyjaśnienie z góry dziękuję . agata: 1. Litery A,B,C,D,E ustawiono w ciąg. Oblicz prawdopodobieństwo , że litere B poprzedza bespośrednio literę D. 2. Dane są dwa pojemniki. W pierwszym są 4 kule białe i 3 czarne, w drugim 5 białych i 4 czarne. Z losowo wybranego pojemnika losujemy 1 kulę. Oblicz prawdopodobieństwo wylosowania kuli czarnej. 3. Z klasy w której jest 8 chłopców i 14 dziewczynek wybrano 5−cio osobową delegację. a− ile takich delegacji można utworzyć b − są same dziewczynki c − dokładnie jedna dziewczynka d − co najwyżej jedna dziewczynka 4.Litery A,B,C,D,E,F,G,H ustawiamy w szeregu. a − ile jest takich ustawień b− ile , że D stoi na pierwszym miejscu c − litera B stoi na pierwszym , a litera F na trzecim

Radosław 2: ad1 Według mnie to będzie tak: P=⁴_5!=¹₃₀.Albo jeśli potraktować problem po żydowsku P=¹₁₅

Eta: Radosław, no coś nie tak ? 1/ poprawne rozwiązanie : |Ω| = 5! = 120 zdarzenieA −− litery BD mogą przemieścić się(razem złączone) na 4 pozycjach w tym ciągu a pozostałe litery : A, C, E −− dowolnie na 3!= 6 sposobów z reguły mnożenia: | A|= 4*6 = 24

	24		1
P(A)=		=
	120		5

Eta:

	1
2/ wybór pojemnika z prawdopodobieństwem p=
	2

	4
wybór kuli białej z I pojemnika z prawdopodobieństwem p=
	7

	5
wybór kuli białej z II pojemnika z prawdop. p=
	9

zdarzenie A −−− wybrano kulę białą ( z pierwszego lub z drugiego pojemnika)

	1		4		1		5
P(A) =		*		+		*		= ....... dokończ obliczenia
	2		7		2		9

zad3/ 8 chł. i 14 dz. R− m 22 uczniów a) wybieramy 5 osób z całej klasy

	22 5		22!
		=		= ............ dokończ .. = 26 334 takich delegacji
			5!*17!

b)same dziewczynki , czyli 5 z 14

	14 5		14!
		=		=........ dokończ
			5!*9!

c) dokładnie jedna dziewczynka, czyli 1 dziewczynka i 4 chł.

	14 1		8 4
		*		= ......... dokończ

d) co najwyżej jedna dziewczynka, czyli 1 dz. i 4chł. lub sami chłopcy

	14 1		8 4		8 5
		*		+		=........ dokończ

Eta: zad.4/ a) wszystkich liter jest 8 możemy je poprzestawiać na 8! sposobów = 1*2*3*4*5*6*7*8= ..... takich ustawień b) D ustawiamy na pierwsze miejsce, pozostałe 7 liter przestawiamy na 7! sposobów mamy 1*7! = ....... dokończ c) B na pierwszym F na trzecim, to pozostałych 6 liter na 6! sposobów mamy: 1*1*6!= ........ powodzenia

Radosław 2: Sorki, Eta i Agata.Taka aszybka.Charakterystyczna,będę pamiętał ! Zadanie to można również rozwiązać w następujący sposób: |Ω|−liczba zdarzeń elementarnych polegających na wyborze 2 miejsc z 5 z

	5 2
uwzględnieniem kolejności miejsc 2*

A−liczba zdarzeń sprzyjających−litery na czterech pozycjach w ciągu P(A)=^A_|Ω| No teraz chyba jest dokładnie