Zadanka
Godzio:
Zadania dla TOmka i Maćka
1. Rozwiąż równanie x
2 = y
2 + 2y + 13 w liczbach całkowitych x, y.
2. Wykaż że w trójkącie o bokach a,b,c i wysokościach odpowiednio h
a,h
b,h
c zachodzi równość:
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
(a + b + c)( |
| + |
| + |
| ) = (ha + hb + hc)( |
| + |
| + |
| ) |
| | a | | b | | c | | ha | | hb | | hc | |
3. Udowodnij że dla dowolnych liczb nieujemnych a,b,c zachodzi nierówność
(a + b)(b + c)(c+a) ≥ 8abc
4. Niech a i b będą liczbami rzeczywistymi. Udowodnij, ze jeśli ax
2−ax−b < 0 dla każdego
rzeczywistego x, to również
|x − a| + b > 0
17 sie 14:04
TOmek: po prostu nie nawidze takich typow zadan, masakra. Gdyby takie coś dali na maturze roz. nawet
bym tego nie ruszył.
1. Rozwiąż równanie x2 = y2 + 2y + 13 w liczbach całkowitych x, y.
x2=y(y+2)+1+12
x2=y2 + 2y+1+12
x2=(y+1)2+12
x2−(y+1)2=12
wniosek jest nastepujący: kompletnie nie wiem co dalej robić
17 sie 14:11
TOmek: 
17 sie 14:11
Godzio:
x2 − (y + 1)2 = ( ... )( ... ) = 12
i co z tego wynika ?
17 sie 14:12
Godzio:
Po to tu jesteś żeby ruszyć takie zadania

17 sie 14:12
Godzio:
Ale to też nie powinieneś się tak od razu poddawać ja nad niektórymi zadaniami które
Eta
mi dawała siedziałem czasami nawet 2 h i w końcu dochodziłem do rozwiązania, liczy się to
żebyś sam pomyślał

17 sie 14:14
Maciek: x2−(y+1)2=12
[x−(y+1)][x+(y+1)]=12
(x−y−1)(x+y+1)=12
17 sie 14:14
Maciek: Tyle wystarczy ,czy dalej coś trzeba zapisać

?
17 sie 14:16
TOmek: widze ,ze kolega nie moj poziom ^^
17 sie 14:17
Maciek: 
coś Ty nie żartuj

17 sie 14:18
Maciek: Wezmę się za to 3

17 sie 14:18
Godzio: to nie koniec
Polecenie: rozwiąż równanie
a wyników nie widzę

17 sie 14:22
Godzio:
Wystarczy się skupić :
a * b = 12 −−−− a, b ∊ C
a = ? i b = ?
v
a = ? i b = ?
v
a = ? i b = ?
v
...
17 sie 14:23
Maciek:
a * b =12
Możliwości są takie

no i wtedy gdy obie liczby są ujemne , ale to chyba nie oto chodzi ,żebu
wypisać 12 możliwości?
4 * 3 =12
3 * 4 =12
1 * 12 =12
12 * 1 = 12
2 * 6 =12
6 * 2 =12
17 sie 14:32
Godzio:
no i ok teraz wracaj do tamtego i twórz układy równań
np.
4 * 3 = 12
x − y − 1 = 4 i x + y + 1 = 3 pamiętając że x,y ∊ C
17 sie 14:34
Maciek:
x−y−1=4
x−y=5
x=5+y
5+y+y+1=3
2y=−3
17 sie 14:42
Maciek: I tak trzeba wszystkie liczyć

?
17 sie 14:42
Godzio:
dokładnie, teraz oblicz wszystko i podaj wyniki
17 sie 14:45
Maciek: A masz wyniki gdzieś bo zanim to tutaj rozpisze a tak bym Ci liczby podał

?
17 sie 14:51
Godzio: no o to chodzi żebyś liczby podał

17 sie 14:52
Maciek: (−4,−1),(4,1),(4,−3),(−3,−4),(−4,1)

17 sie 15:05
Godzio: (−4,−1) − odpada
(−3,−4) −> chyba miało być (−4,−3)

17 sie 15:09
Maciek: Możliwe bo liczyłem to szybko i nie sprawdzałem

17 sie 15:10
Godzio: To teraz kolejne próbuj, ale postaraj się nie pisać kilka razy
bzdur 
tylko od razu
poprawne rozwiązanie 2 i 4 jest proste przy 3 trzeba chwilkę pomyśleć

17 sie 15:12
Maciek: 2 to dla mnie czarna magia

Nie mam pojęcia kompletnie jak udowadniać takie zadania.
W 4 domyślam się ,że z ax
2−ax−b<0 wyciągamy Δ i wtedy:
a
2+4ab<0
a(a+4b)<0 /:(a+4b)
a<0 , ale nie wiem co to nam daje

Z kolei wartość bezwzględną również można opuścić i otrzymujemy:
Ix−aI+b>0
x − a + b > 0 v −x + a + b > 0
P.S. Wiem Godziu ,że Cię zawodzę

17 sie 15:31
Godzio:
po pierwsze nie możesz dzielić przez (a + 4b) bo nie wiesz czy jest dodatnie czy ujemne
po drugie a < 0 to wynika z treści zadania
po 3 |x − a| + b > 0 − wystarczy jakoś pokazać że b > 0 bo |x − a| ≥ 0
17 sie 15:45
Godzio:
Jeśli żadnego nie ruszycie to około 20 napisze rozwiązania, no chyba że ktoś inny już to zrobi

, ale najlepiej by było gdybyście rozwiązali te zadania
17 sie 16:52
Maciek: Godzio wolałbym ,żebyś rozwiązania podał później około północy

bo później jeszcze będę
próbował

17 sie 16:56
Godzio: no to dobra

17 sie 16:57
Maciek:
Dobra Godziu poddaje się

Odnośnie 4. zadania poddaj mi jak wykazać ,że to b>0.
A w 2. zadaniu przypuszczam ,że 8abc można jakoś inaczej zapisać pewnie z jakiegoś wzoru , ale
nie wpadłem jak

17 sie 23:20
think: Maciek bo nie wiesz, że Godzio kocha zadania z takim faktem, że średnia arytmetyczna ≥ średniej
geometrycznej
17 sie 23:31
think: (a + b)(b + c)(c + a) ≥ 8abc / : 8
| a + b | |
| ≥ √ab pozostałe ułamki tak samo |
| 2 | |
i otrzymamy:
| a + b | b + c | c + a | |
|
|
| ≥ √ab*√bc*√ca = abc |
| 2 | 2 | 2 | |
17 sie 23:34
think: co do czwartego zadania to wystarczy podać warunki dla funkcji kwadratowej.
a < 0 i Δ < 0 ponieważ wartości funkcji są ujemne, a to znaczy, że ramiona paraboli będą
skierowane w dół i parabola nie ma miejsc zerowych, zgadza się?
17 sie 23:41
Maciek: Zgadza się

17 sie 23:45
think: no to skoro mi już przyznajesz rację... to może porządnie rozwiążesz to zadanie tak od początku
do końca

wiesz tak, żeby mi się lżej spało po dobrze udzielonej podpowiedzi

17 sie 23:48
Godzio: a ja proponuje coś takiego:
f(0) = − b < 0 ⇒ b > 0 koniec dowodu

17 sie 23:53
Godzio:
No to jeszcze zostało zadanie 2

, kto chętny ?
17 sie 23:54
Godzio:
To wy dumajcie a ja idę dumać nad Widzew − Wisła = Remis

17 sie 23:54
Maciek: Godzio na czym obstawiasz

?
17 sie 23:55
think: Maciek Ty chyba nie wiesz o co chodzi

to kryptarytm

17 sie 23:57
Maciek: No to think spróbuję to zapisać jakoś

18 sie 00:01
think: to do dzieła

18 sie 00:03
Maciek:
ax
2−ax−b<0
Δ=a
2+4ab
Δ
a=0−4*1*4ab
Δ
a<0
Nie wiem jak to a pokazać... wrrr

18 sie 00:09
Godzio:
Maciek które będzie zadanie teraz zapisywać

?
18 sie 00:10
Godzio:
nieco wyżej napisałem rozwiązanie

ax
2 − ax − b < 0 dla x ∊ R
f(0) < 0
−b < 0
b > 0
więc |x − a| + b > 0 c.n.d.
18 sie 00:11
think: Maciek pamiętasz warunek?
a < 0 i Δ < 0
także wylicz b z
a2 + 4ab < 0
18 sie 00:12
Maciek: Godziu Twoje wyjaśnienie jest jasne , ale Think stwierdziła ,że można pokazać Δ<0 i a<0.
18 sie 00:12
think: nom szybszy sposób.

zresztą przeważnie prezentujesz ładne rozwiązania

18 sie 00:13
Maciek:
a(a+4b)<0/:a
a+4b<0
4b<−a
18 sie 00:14
think: no to przedstawiam moje rozwiązanie:
Δ = a
2 + 4ab
Δ < 0
a
2 + 4ab < 0
a(a + 4b) < 0 ponieważ a < 0 to też warunek to aby tam otrzymać liczbę ujemną z tego mnożenia
to
| | a | |
a + 4b >0 ⇒ b > − |
| ⇒ b > 0 |
| | 4 | |
18 sie 00:16
think: Maciek podzieliłeś przez a, które jest ujemne i nie zmieniłeś znaku nierówności.
18 sie 00:16
Maciek: No ok ,ale w którym miejscu z zadania wyczytałaś a<0? bo przez to mi całe zadanie nie wyszło.
18 sie 00:18
think:
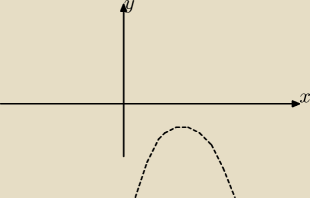
"Udowodnij, ze jeśli ax
2−ax−b < 0 dla każdego rzeczywistego x..."
f(x) = ax
2 − ax − b
masz udowodnić, że jeśli f(x) < 0 dla każdego x, a kiedy wartości funkcji kwadratowej są ujemne
? bo f(x) < 0 oznacza właśnie to, że wartościami funkcji są tylko liczby ujemne.
Rysunek poglądowy...
18 sie 00:24
Maciek: No wartości funkcji kwadratowej są ujemne wtedy gdy ramiona są skierowane w dół , a więc a<0 i
Δ<0.
18 sie 00:27
think: no i co doszedłeś do warunku że a < 0

18 sie 00:28
Godzio:
Dziękuję bardzo
think za kwiatka

... za rybę też chodź już dzisiaj jadłem

18 sie 00:31
Maciek: A można to wyznaczyć , czy to po prostu wystarczy wyczytać?
18 sie 00:31
Godzio:
to już mówi samo przez się:
ax2 − ax − b < 0 dla x ∊ R więc muszą być spełnione 2 warunki: a < 0 i Δ < 0
18 sie 00:35
Maciek: Acha, "samo przez się" , po raz kolejny rzeczy dla was oczywiste dają mi do myślenia i.. dobrze

Chociaż się czegoś od was nauczę , Dzięki

18 sie 00:38
think: no nie Maciek, po prostu w tym wypadku tak się składa, że a ze wzoru ogólnego funkcji
kwadratowej pokrywa się z a z zadania, gdybyś miał:
dx2 − dx − b < 0 to byłby warunek że a < 0 czyli w zadaniu to d < 0 tak? teraz to widzisz?
18 sie 00:41
Godzio:
Często się też zdarzają takie zadania na maturze np:
Dla jakiej wartości parametru m nierówność jest spełniona przez każdego rzeczywistego x:
mx2 + mx − 5 + m < 0
18 sie 00:41
Godzio: i wtedy musisz podać te 2 warunki
a < 0 i Δ < 0
i znaleźć część wspólną
18 sie 00:41
Godzio: w tym wypadku co podałem to akurat jest jeszcze m = 0 rozwiązaniem

, ale takie zadania możesz
się jak najbardziej spodziewać na rozszerzeniu
18 sie 00:43
think: dobra


idę spać, bo jutro a właściwie dziś będzie trzeba uczciwie popracować...w
sensie odwalić większy kawał roboty, bez sugestii jakobym była oszustką

18 sie 00:48
Maciek: Mógłbyś mi rozwiązanie napisać

?
18 sie 00:49
Maciek: Bo chciałbym to jeszcze przejrzeć od góry do dołu

18 sie 00:50
Maciek: 
think , Dobranoc

18 sie 00:50
Godzio: które zadanie ?
18 sie 00:51
Maciek: to teraz co podałeś

18 sie 00:52
Eta:
Miłego odpoczynku


Dobranoc

18 sie 00:53
Godzio:
mx
2 + mx − 5 + m < 0
a < 0 ⇒ m < 0
Δ < 0
m
2 − 4m(m − 5) < 0
m
2 − 4m
2 + 20m < 0
−3m
2 + 20m < 0
m(3m − 20) > 0
m = 0
0 + 0 − 5 + 0 < 0
−5 < 0
Odp: m ∊ (−
∞,0>
18 sie 00:54
Godzio:

18 sie 00:55
Maciek: To nie jest trudne

kojarzę to z początku 2 klasy

18 sie 00:59
Maciek: a jeśli mx2 +mx −5 +m > 0 to wtedy było by a>0⇒m>0 ?
18 sie 01:00
Godzio: tak jest i do tego Δ < 0
18 sie 01:03
Maciek: A kiedy będzie Δ>0?
18 sie 01:05
Godzio: kiedy bedą 2 rozwiązania

18 sie 01:05
Maciek: A kiedy poznam po zadaniu ,że będzie Δ=0 czyli 1 rozwiązanie , Δ<0 czyli część wspólna , Δ>0
czyli 2 rozwiązania ?
18 sie 01:07
Godzio: a to zależy już od treści zadania
18 sie 01:08
Maciek: Dla jakiej wartości parametru m nierówność jest spełniona przez każdego rzeczywistego x:
mx2 + mx − 5 + m < 0 , Tu akurat po czym poznajemy ,że Δ<0?
18 sie 01:10
think: Maciek po tym, że nierówność jest ostra

18 sie 01:13
Maciek: A po czym poznajemy ,że nierówność jest ostra

?
18 sie 01:13
Maciek: Po znaku? > lub < ?
18 sie 01:14
Maciek: A jak jest ≤ lub ≥ to nierówność jest nieostra i wtedy Δ>0? A jak jest znak = to Δ=0?
18 sie 01:17
think: nie

jeśli jest np mx
2 + mx − 5 + m ≤ 0
to Δ ≤ 0

18 sie 01:18
think: natomiast zadania w których Δ > 0 może być sformułowane np w taki sposób: funkcja osiąga max w
czwórce.
18 sie 01:20
Godzio:
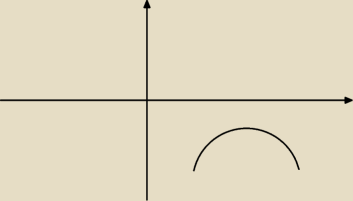
albo po tym że sokoro jest cała pod osią OX to w takim razie nie ma miejsc zerowych a skoro nie
ma miejsc zerowych to Δ < 0 i kropka
18 sie 01:20
Maciek: Ale to już jest np. nierówność nieostra ,a Δ≤0

? to kiedy jest większa od 0

?
18 sie 01:20
Godzio:
Poczekaj Maciek, zaraz poszukam mam takie zadanka z tego typu rzeczami napisze Ci kilka
przykładów i zobaczysz o co kaman
18 sie 01:21
think: albo funkcja ma dwa różne pierwiastki, no i wychodzi warunek Δ > 0
18 sie 01:21
Maciek: Jeśli mx2 +mx −5 +m > 0 to wtedy było by a>0⇒m>0 ? i Δ<0? to wtedy będą miejsca zerowe

? więc
mi nie pasuje

18 sie 01:22
Maciek: No daj Godzio to zrobię

18 sie 01:23
think: a kto powiedział, że będą miejsca zerowe

? przecież Δ < 0
18 sie 01:23
Maciek: Aaa no tak to wtedy będą ramiona do góry i wykres będzie nad OX.
18 sie 01:25
think: aa serce czujesz

18 sie 01:26
Maciek: Godziu napisz mi coś jak będziesz miał chwilę to jutro(dzisiaj) coś pomęczę, a ja lecę spać


18 sie 01:26
Maciek: serce czujesz


18 sie 01:27
think: leć, ja też może w końcu jakoś pokonam te 3 metry które dzielą mnie od spania

18 sie 01:27
Godzio:
1.Dla jakich wartości parametru m nierówność mx2 − (2m − 1)x + 2m − 1 > 0
jest prawdziwa dla każdego x ∊ R
Warunki do rozwiązania:
a > 0, Δ < 0
2. Dla jakich wartości parametru m nierówność (m−1)x2 − (6 − 4m)x + 2 < 0
jest prawdziwa dla każdego x ∊ R
Warunki do rozwiązania:
a < 0, Δ < 0
3. Dla jakich wartości parametru m równanie (m2 + 3m − 10)x2 − 2(m−2)x − 1 = 0
ma 2 różne pierwiastki.
Δ > 0
4.Dla jakich wartości parametru m nierówność mx2 − x + m − 1 > 0
nie posiada rozwiązania
a < 0, Δ < 0
I jedno takie ogólne:
5. Zbadaj liczbę pierwiastków równania w zależności od parametru m:
(m + 4)x2 − 4mx + 3m = 0
1o 0 rozwiązań: a < 0 i Δ < 0 lub a > 0 i Δ < 0
2o 1 rozwiązanie: Δ = 0 i a ≠ 0, przypadek m = −4 trzeba rozpatrzyć osobno
3o 2 rozwiązania: Δ > 0 i a ≠ 0
18 sie 01:28
think: Maciek widziałeś reklamę z mózgiem i sercem?
Serce prosi mózg aby mu coś wytłumaczył, a ono ciągle, tylko odpowiada, że nie czuję tego

a
na końcu się pyta czy to będzie tak szybko jak rozpiąć zamek w sukience, mózg, że tak i serce
na to:
aaaa to czuję to, czuję....
18 sie 01:29
Godzio:
No to ładnie ja tu się produkuję a ten poszedł spać

18 sie 01:29
think: Godzio don't worry jestem pewna w 99%, że jutro wstanie i obejrzy efekty produkcji

18 sie 01:31
Maciek: W 4. nie powinno być a>0?
18 sie 01:31
Godzio: popatrz na polecenie
18 sie 01:31
think: no i widzisz jak wyczuł świetnie

18 sie 01:31
Godzio:
Mam nadzieję że do 13 wszystko będzie zrobione

bo jakoś tak wstanę zobaczę, ewentualnie
poprawię i lecę na rowerek

18 sie 01:32
think: tylko pięć zadań, no co Ty

18 sie 01:33
Godzio:
EJ

ale zostało jeszcze 2 zadanie bo my tak gadu gadu a zadanie czeka

18 sie 01:33
Maciek: Widzę polecenie ,ale jest 0 rozwiązań dla a>0 i a<0 to dlaczego tam jest a<0 ?
18 sie 01:33
Maciek: 2 nie umiem

18 sie 01:34
Godzio:
ale to teraz o którym mówisz

4 czy 5 ?
18 sie 01:34
think: ponieważ polecenie brzmi dla jakich wartości parametru m nierówność nie ma rozwiązania
18 sie 01:35
Maciek: No 4 cały czas.
18 sie 01:35
think: ale to może zostawmy na jutro wtedy pogadamy o zaprzeczeniu, do tej pory mówiliśmy tylko o
zadaniach gdzie miałeś pokazać, że tak jest.
18 sie 01:36
Maciek: Think wiem ,że jest napisane ,że nie ma , ale wtedy Δ<0 i a<0 lub a>0 to dlaczego akurat jest
a<0 a nie a>0?
18 sie 01:36
Godzio:
bo jeśli a > 0 to na pewno nierówność będzie miała jakieś rozwiązanie
think idź lepiej spać bo naprawdę poranek będzie ciężki a my możemy spać ile wzlezie

18 sie 01:36
think: dobra finito jeszcze raz

i zmiatam, do zobaczenie o jakiejś normalniejszej porze

18 sie 01:37
Maciek: 0 rozwiązań: a < 0 i Δ < 0 lub a > 0 i Δ < 0 ? to dlaczego tu jest a>0 i Δ<0?
18 sie 01:38
Godzio:
18 sie 01:38
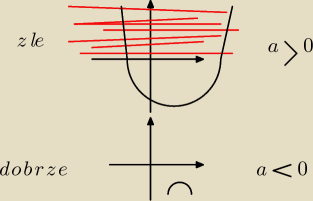
Godzio:
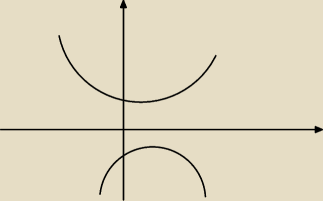
bo może być z ramionami albo do dołu albo do góry

18 sie 01:39
Maciek: Godziu , ale jeśli a>0 i Δ<0 to wykres w tym "złym" nie powinien być nad osią OX?
18 sie 01:40
Maciek: No i w obu przypadkach a<0 lub a>0 jest 0 rozwiązań?
18 sie 01:40
Godzio:
to co czerwone tyczy się zadania czwartego, w zakreskowanym polu nierówność ma rozwiązanie
więc a > 0 nie wchodzi w grę
18 sie 01:41
Maciek: Skoro a>0 i Δ<0 to wykres nie powinien być nad osią OX?
18 sie 01:42
Godzio:
Maciek lepiej się z tym prześpij i rano przeanalizuj,
... = 0 − rozwiązania są wtedy gdy wykres przecina oś OX
... > 0 − rozwiązania są wtedy gdy wykres chodź trochę jest ponad osią OX
... < 0 − gdy wykres jest pod osią
18 sie 01:42
Maciek: I wtedy brak rozwiązań?
18 sie 01:42
18 sie 01:43
Maciek: No i zobacz 1 obrazek

tak jak mówię kiedy a>0 i Δ<0 to 0 rozwiazan?
18 sie 01:44
Godzio:
te warunki a ... 0 , Δ ... 0
zależą od znaku czy jest to ">", "<", "≤", "≥", "=" i od polecenie robiąc kilka przykładów
myślę że sobie to przyswoisz
18 sie 01:44
Godzio:
To co napisałem ( Warunki do rozwiązania: ... ) są na pewno dobrze także z tym nie ma się co
kłócić

18 sie 01:45
Maciek: Okey ale odpowiedz mi na moje pytanie , Kiedy a>0 i Δ<0 to jest 0 rozwiązań?
18 sie 01:46
Godzio:
jeśli mx2 + ... < 0
to tak
18 sie 01:48
Maciek: Poddaje się na teraz

Zrobię to i może przejrzę na oczy. Dobranoc

18 sie 01:50
Godzio: No do następnego
18 sie 01:58
Maciek:
mx
2 − (2m − 1)x + 2m − 1 > 0
Zał. a<0⇒m<0 , Δ<0
Δ=−1
2(2m−1)
2−4*m*(2m−1)
Δ=4m
2−4m+1−8m
2+4m
Δ=−4m
2+1
−4m
2+1<0/*(−1)
4m
2−1>0
(2m−1)(2m+1)>0
Narazie jedno bo nie mam czasu chwilowo

, dobrze chociaż?
18 sie 13:09
Maciek: | | 1 | | 1 | |
m∊(− |
| ; |
| ) −>poprawka  |
| | 2 | | 2 | |
18 sie 13:09
Godzio:
Rozwiązaniem musi być część wspólna

(pomijając że końcowa nierówność z m ma inne
rozwiązanie)
| | 1 | |
sprawdź przypadek m = |
| czy też będzie się zgadzać |
| | 2 | |
18 sie 13:26
Godzio:
ale nierówność ma być zawsze prawdziwa więc a > 0
18 sie 13:27
TOmek:
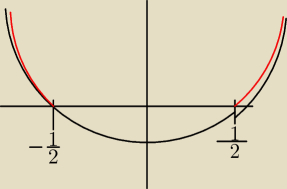
(2m−1)(2m+1)>0
| | 1 | | 1 | |
m∊(− ∞,− |
| ) v ( |
| , ∞) |
| | 2 | | 2 | |
18 sie 13:31
TOmek: pomęcze sie z Mackiem

18 sie 13:31
Maciek: No okey Godziu ale w warunkach było a<0 więc jak ma wkońcu być?
18 sie 13:33
Godzio:
ok, i pamiętajcie zawsze z równaniami z parametrem patrzcie czy jeśli dobierzemy tak parametr m
| | 1 | |
żeby jedna potęga się wyzerowała to możemy otrzymać rozwiązanie, i w tym wypadku m = |
| |
| | 2 | |
też jest prawidłowe − x się zeruje, wyraz wolny też i zostaje
| 1 | |
| x 2 > 0 − a to jest zawsze prawdziwe  |
| 2 | |
18 sie 13:34
Godzio:
popatrz dokładniej bo ja tam nie widze a < 0

18 sie 13:34
Maciek: W założeniach?
18 sie 13:35
Godzio:
tak, zobacz na pierwsze zadanie
18 sie 13:36
Maciek: Źle napisałem... no to wtedy by się zgadzało ,że ramiona do góry.A w którym miejscu jest źle
policzone w Δ?
18 sie 13:38
Godzio:
jest dobrze wszystko tylko odpowiedź była zła
18 sie 13:38
Maciek: Ok zrobię resztę później

18 sie 13:44
Maciek:
(m−1)x
2 − (6 − 4m)x + 2 < 0
Zał.a<0 i Δ<0
Δ=−1
2(6−4m)
2−4*(m−1)*2
Δ=36−48m+16m
2−8m+8
Δ=16m
2−56m+44
Δ
m=3136−4*16*44
Δ
m=3136−2816
Δ
m=320
Δ
m=8
√5
| | 56−8√5 | | 56+8√5 | |
m1= |
| m2= |
| |
| | 32 | | 32 | |
| | 8(7−√5) | | 8(7+√5) | |
m1= |
| m2= |
| |
| | 32 | | 32 | |
18 sie 22:51
Godzio:
Maciek rób zadanka ja będę później to sprawdzę

18 sie 22:54
Maciek:
3.(m2 + 3m − 10)x2 − 2(m−2)x − 1 = 0
Zał.Δ>0
Δ=−22(m−2)2−4*(m2 + 3m − 10)*(−1)
Δ=4*(m2−4m+4)−(−4m2+12m−40)*(−1)
Δ=4m2−16m+16−(4m2−12m+40)
Δ=4m2−16m+16−4m2+12m−40
Δ=−4m−24
4m−24>0
4m>24
m>6
m∊(6,+∞)
18 sie 22:58
Godzio:
tylko pamiętaj rozwiązania to część wspólna, m < 1 + Δ => ....
18 sie 23:01
Godzio: w 3 poknociłeś z minusem coś popraw ... ja lecę będę koło 1
18 sie 23:02
Maciek: 4.
mx
2 − x + m − 1 > 0
Zał.a<0 i Δ<0
Δ=(−1)
2−4*m*(m−1)
Δ=1−4m
2+4m
Δ=−4m
2+4m+1
Δ
m=16−4*(−4)*1
Δ
m=32
√Δm=
√32
√Δm=4
√2
| | −4−4√2 | | −4+4√2 | |
m1= |
| m2= |
| |
| | −8 | | −8 | |
| | −4(1+√2) | | −4(1−√2) | |
m1= |
| m2= |
| |
| | −8 | | −8 | |
18 sie 23:13
Maciek:
3.
−4m−24>0
−4m>24/:(−4)
m<−6
m∊(−
∞;−6)
Zapomniałem minusa spisać

18 sie 23:15
Maciek:
5.
(m + 4)x2 − 4mx + 3m = 0
Domyślam się ,że trzeba podać pierwiastki dla m=0,m<0 i m>0
1o
Dla m=0
4x2=0 /:4
x2=0
x=0
2o
Dla m<0
(m + 4)x2 − 4mx + 3m < 0
Zał.a<0⇒m<0 i Δ>0
Δ=16m2−4*(m+4)*(3m)
Δ=16m2−4(3m2+12)
Δ=16m2−12m2−48
Δ=4m2−48
4m2−48<0/:(4)
m2−12<0
(m−2√3)(m+2√3)<0
m∊(−2√3;2√3)
3o
Dla m>0
(m + 4)x2 − 4mx + 3m < 0
Zał.a>0⇒m>0 i Δ>0
Δ=16m2−4*(m+4)*(3m)
Δ=16m2−4(3m2+12)
Δ=16m2−12m2−48
Δ=4m2−48
4m2−48>0/:(4)
m2−12>0
(m−2√3)(m+2√3)>0
m∊(−∞;2√3)∪(2√3;+∞)
18 sie 23:34
Maciek: Zrobiłem jak myślałem ,ale pewnie będziesz miał dużo poprawiania Godziu więc się nie przejmuj

.Jeszcze mam rok to się nauczę

18 sie 23:35
Godzio: 3. dalej źle jest
4. odpowiedź

część wspólna z a<0 i Δ < 0

oba warunki mają być spełnione a nie tylko jeden
5 sprawdzę później ale już widzę że chyba coś nie tak rób powoli i dokładnie żeby 100 razy nie
powtarzać
18 sie 23:38
Maciek: Poprawię to 3 jutro,a w 4 nie wiem jak zapisać część wspólną a<0 i Δ<0.
19 sie 00:08
Godzio:
m< 0 i ten przedział da nam odpowiedź:
19 sie 00:13



 ?
?
 coś Ty nie żartuj
coś Ty nie żartuj 


 no i wtedy gdy obie liczby są ujemne , ale to chyba nie oto chodzi ,żebu
wypisać 12 możliwości?
4 * 3 =12
3 * 4 =12
1 * 12 =12
12 * 1 = 12
2 * 6 =12
6 * 2 =12
no i wtedy gdy obie liczby są ujemne , ale to chyba nie oto chodzi ,żebu
wypisać 12 możliwości?
4 * 3 =12
3 * 4 =12
1 * 12 =12
12 * 1 = 12
2 * 6 =12
6 * 2 =12
 ?
?
 ?
?




 tylko od razu
poprawne rozwiązanie 2 i 4 jest proste przy 3 trzeba chwilkę pomyśleć
tylko od razu
poprawne rozwiązanie 2 i 4 jest proste przy 3 trzeba chwilkę pomyśleć 
 Nie mam pojęcia kompletnie jak udowadniać takie zadania.
W 4 domyślam się ,że z ax2−ax−b<0 wyciągamy Δ i wtedy:
a2+4ab<0
a(a+4b)<0 /:(a+4b)
a<0 , ale nie wiem co to nam daje
Nie mam pojęcia kompletnie jak udowadniać takie zadania.
W 4 domyślam się ,że z ax2−ax−b<0 wyciągamy Δ i wtedy:
a2+4ab<0
a(a+4b)<0 /:(a+4b)
a<0 , ale nie wiem co to nam daje  Z kolei wartość bezwzględną również można opuścić i otrzymujemy:
Ix−aI+b>0
x − a + b > 0 v −x + a + b > 0
P.S. Wiem Godziu ,że Cię zawodzę
Z kolei wartość bezwzględną również można opuścić i otrzymujemy:
Ix−aI+b>0
x − a + b > 0 v −x + a + b > 0
P.S. Wiem Godziu ,że Cię zawodzę 
 , ale najlepiej by było gdybyście rozwiązali te zadania
, ale najlepiej by było gdybyście rozwiązali te zadania
 bo później jeszcze będę
próbował
bo później jeszcze będę
próbował 

 Odnośnie 4. zadania poddaj mi jak wykazać ,że to b>0.
A w 2. zadaniu przypuszczam ,że 8abc można jakoś inaczej zapisać pewnie z jakiegoś wzoru , ale
nie wpadłem jak
Odnośnie 4. zadania poddaj mi jak wykazać ,że to b>0.
A w 2. zadaniu przypuszczam ,że 8abc można jakoś inaczej zapisać pewnie z jakiegoś wzoru , ale
nie wpadłem jak 

 wiesz tak, żeby mi się lżej spało po dobrze udzielonej podpowiedzi
wiesz tak, żeby mi się lżej spało po dobrze udzielonej podpowiedzi 

 , kto chętny ?
, kto chętny ?

 ?
?
 to kryptarytm
to kryptarytm 



 ?
?
 ax2 − ax − b < 0 dla x ∊ R
f(0) < 0
−b < 0
b > 0
więc |x − a| + b > 0 c.n.d.
ax2 − ax − b < 0 dla x ∊ R
f(0) < 0
−b < 0
b > 0
więc |x − a| + b > 0 c.n.d.
 zresztą przeważnie prezentujesz ładne rozwiązania
zresztą przeważnie prezentujesz ładne rozwiązania 
 "Udowodnij, ze jeśli ax2−ax−b < 0 dla każdego rzeczywistego x..."
f(x) = ax2 − ax − b
masz udowodnić, że jeśli f(x) < 0 dla każdego x, a kiedy wartości funkcji kwadratowej są ujemne
? bo f(x) < 0 oznacza właśnie to, że wartościami funkcji są tylko liczby ujemne.
Rysunek poglądowy...
"Udowodnij, ze jeśli ax2−ax−b < 0 dla każdego rzeczywistego x..."
f(x) = ax2 − ax − b
masz udowodnić, że jeśli f(x) < 0 dla każdego x, a kiedy wartości funkcji kwadratowej są ujemne
? bo f(x) < 0 oznacza właśnie to, że wartościami funkcji są tylko liczby ujemne.
Rysunek poglądowy...

 ... za rybę też chodź już dzisiaj jadłem
... za rybę też chodź już dzisiaj jadłem 
 Chociaż się czegoś od was nauczę , Dzięki
Chociaż się czegoś od was nauczę , Dzięki 
 , ale takie zadania możesz
się jak najbardziej spodziewać na rozszerzeniu
, ale takie zadania możesz
się jak najbardziej spodziewać na rozszerzeniu

 idę spać, bo jutro a właściwie dziś będzie trzeba uczciwie popracować...w
sensie odwalić większy kawał roboty, bez sugestii jakobym była oszustką
idę spać, bo jutro a właściwie dziś będzie trzeba uczciwie popracować...w
sensie odwalić większy kawał roboty, bez sugestii jakobym była oszustką 
 ?
?

 think , Dobranoc
think , Dobranoc 


 Dobranoc
Dobranoc

 kojarzę to z początku 2 klasy
kojarzę to z początku 2 klasy 


 ?
?
 jeśli jest np mx2 + mx − 5 + m ≤ 0
to Δ ≤ 0
jeśli jest np mx2 + mx − 5 + m ≤ 0
to Δ ≤ 0 
 albo po tym że sokoro jest cała pod osią OX to w takim razie nie ma miejsc zerowych a skoro nie
ma miejsc zerowych to Δ < 0 i kropka
albo po tym że sokoro jest cała pod osią OX to w takim razie nie ma miejsc zerowych a skoro nie
ma miejsc zerowych to Δ < 0 i kropka
 ? to kiedy jest większa od 0
? to kiedy jest większa od 0 ?
?
 ? więc
mi nie pasuje
? więc
mi nie pasuje 

 ? przecież Δ < 0
? przecież Δ < 0






 a
na końcu się pyta czy to będzie tak szybko jak rozpiąć zamek w sukience, mózg, że tak i serce
na to:
aaaa to czuję to, czuję....
a
na końcu się pyta czy to będzie tak szybko jak rozpiąć zamek w sukience, mózg, że tak i serce
na to:
aaaa to czuję to, czuję....



 bo jakoś tak wstanę zobaczę, ewentualnie
poprawię i lecę na rowerek
bo jakoś tak wstanę zobaczę, ewentualnie
poprawię i lecę na rowerek 

 ale zostało jeszcze 2 zadanie bo my tak gadu gadu a zadanie czeka
ale zostało jeszcze 2 zadanie bo my tak gadu gadu a zadanie czeka 

 4 czy 5 ?
4 czy 5 ?

 i zmiatam, do zobaczenie o jakiejś normalniejszej porze
i zmiatam, do zobaczenie o jakiejś normalniejszej porze 

 bo może być z ramionami albo do dołu albo do góry
bo może być z ramionami albo do dołu albo do góry 
 tak jak mówię kiedy a>0 i Δ<0 to 0 rozwiazan?
tak jak mówię kiedy a>0 i Δ<0 to 0 rozwiazan?

 Zrobię to i może przejrzę na oczy. Dobranoc
Zrobię to i może przejrzę na oczy. Dobranoc 
 , dobrze chociaż?
, dobrze chociaż?

 (pomijając że końcowa nierówność z m ma inne
rozwiązanie)
(pomijając że końcowa nierówność z m ma inne
rozwiązanie)
 (2m−1)(2m+1)>0
(2m−1)(2m+1)>0






 .Jeszcze mam rok to się nauczę
.Jeszcze mam rok to się nauczę 
 część wspólna z a<0 i Δ < 0
część wspólna z a<0 i Δ < 0  oba warunki mają być spełnione a nie tylko jeden
5 sprawdzę później ale już widzę że chyba coś nie tak rób powoli i dokładnie żeby 100 razy nie
powtarzać
oba warunki mają być spełnione a nie tylko jeden
5 sprawdzę później ale już widzę że chyba coś nie tak rób powoli i dokładnie żeby 100 razy nie
powtarzać