Calka Marcin: Mam prośbę czy mogłby ktoś rozwiązać takie oto zadanie bo nie bardzo wiem jak sie za to zabrać Zadanie z działu całek podwójnych obliczanie objętosci 1. z=xy x+y+z=1 z=0 2 z²=xy x+y=4 x+y=6 Jeżeli ktoś zrobi jedno z tych to będe bardzo wdzięczny i obiecuje ze drugie zrobię sam a przynajmniej sie postaram

AS: Podaję rozwiązanie − bez gwarancji Zad. 1 Granice całkowania dla x: 0 ... 1 Granice całkowania dla y: 0... 1 − x Granice całkowania dla z; 0 ... xy 1 1 − x 1 1 − x 1 1 − x V = ∫ ∫ xydxdy = ∫xdx∫ ydy = ∫xdx [y²/2] | = 0 0 0 0 0 0 1 1 1/2∫ x*[(1 − x)² − 0²]dx = 1/2∫(x − 2*x² + x³)dx = 0 0 1 1/2[x²/2 − 2x³/3 + x⁴/4] = 1/2[1/2 − 2/3 + 1/4 − 0 + 0 − 0] = 0 1/2*[6/12 − 8/12 + 3/12] = 1/2*1/12 = 1/24 Odp. V = 1/24

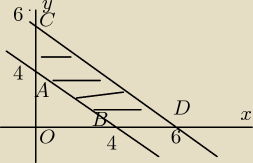
AS: Zad.2 Szukana objętosc będzie się znajdować nad obszarem zakreskowanym. Obszar całkowania znajdziemy jako różnicę pól trójkątów OCD i OAB czyli V1 to objętość nad obszarem OCD,V2 to objętość nad obszarem OAB Równanie CD: y = 6 − x ; AB y = 4 − x V = V1 − V2 6 6−x 6 6−x V1 = ∫ ∫ √xydxdy = ∫√xdx∫√ydy = 0 0 0 0 6 6−x 6 6−x = ∫ √xdx∫y^1/2dy = ∫√xdx[y^3/2/(3/2)] | 0 0 0 0 dalej pogłówkuj sam Jak wystąpią problemy jutro ciąg dalszy pomocy. Powodzenia.