zadanko na stożka mi: Jaki powinien być stosunek promienia podstawy stożka do jego tworzącej, która ma długość l, aby objętość stożka była największa?

think:

	1
V =		πr2h
	3

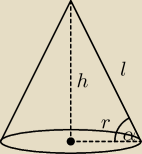
	r
cosα =		⇒ r = lcosα oraz α ∊ (0, 90o)
	l

	h
sinα =		⇒ h = lsinα
	l

	1		1
V =		π(lcosα)2*lsinα =		πl3(1−sin2α)sinα
	3		3

	1
chcemy aby funkcja objętości osiągnęła max		πl3 to są wielkości ustalone, czyli o max
	3

decyduje (1 − sin²α)sinα liczymy pochodną: (sinα − sin³α)' = cosα − 3sin²αcosα = 0 cosα(1 − 3sin²α) = 0 ⇔ cosα = 0 rozwiązanie spoza dziedziny, więc odpada

	1		√3
lub 1 − 3sin2α = 0 ⇒ sin2α =		⇒ sinα =		i tu funkcja osiąga max
	3		3

ale pytają nas o cosα.

	1		2		√6		r
cos2α = 1 −		=		⇒ cosα =		=
	3		3		3		l

mi: dzieki

think: a znasz odpowiedzi do tych zadań?

mi: wyszło dobrze