Zadania egzaminacyjne Bogdan: Zadania egzaminacyjne. Obiecałem wstawić kilka zadań egzaminacyjnych sprzed pół wieku z egzaminów na wyższe uczelnie. Wybrałem zadania z roku 1960 z krótką treścią, zamieszczone są one w publikacji pt.: Zbiór zadań maturalnych i egzaminacyjnych − część trzecia", Stanisław Kartasiński, Mieczysław Okołowicz, Państwowe Zakłady Wydawnictw Szkolnych − Warszawa 1967.

	sin2x		cos23x
1. Rozwiązać równanie:		−		= 4
	sin2x		cos2x

(Uniwersytet Jagielloński w Krakowie)

	cos2x
2. Rozwiązać równanie: cosx + sinx =
	1 − sin2x

(Uniwersytet Jagielloński w Krakowie) 3. Wszystkie ściany równoległościanu są rombami o boku równym a i kącie ostrym α. obliczyć objętość tego równoległościanu. (Uniwersytet Łódzki) 4. Dowieść, że jeżeli k, m, n oraz x są liczbami dodatnimi różnymi od jedności i log_k x, log+m x, log_n x są wyrazami postępu arytmetycznego, to: n² = (kn)^{log_k m} (Uniwersytet im. A. Mickiewicza w Poznaniu) 5. Rozwiązać układ równań: √ x² + y² + √ 2xy = 8√2 i √x + √y = 4 (Uniwersytet im. A. Mickiewicza w Poznaniu) 6. Rozwiązać równanie: tg4x = sin8x (Uniwersytet Warszawski) 7. Rozwiązać równanie: log₄ (x + 12) * log_x 2 = 1 (Uniwersytet Warszawski)

	3
8. Rozwiązać równanie: sin4x + sin4(90o + x) =
	4

(Uniwersytet Wrocławski)

	180o		360o		1
9. Udowodnić równość: cos		* cos		=
	5		5		4

(Uniwersytet Wrocławski) 10. Rozwiązać układ równań: xy = 300 i x^{log y} = 9 (Wyższa Szkoła Pedagogiczna w Katowicach)

think: ad7. log₄(x + 12) *log_x2 = 1 dziedzina: 1^ox + 12 > 0 ⇒ x > −12 2^ox > 0 i x ≠ 1 część wspólna 1^o i 2^o x > 0 i x ≠ 1

	log42
log4(x + 12)*		= 1
	log4x

	1
log4(x + 12)*		= 1 / *log4x2
	log4x2

log₄(x + 12) = log₄x² x + 12 = x² x² − x − 12 = 0 Δ = 1 + 48 = 49 √Δ = 7 x₁ = 4 x₂ = −3 ← odpada, bo nie należy do dziedziny. Rozwiązaniem jest x = 4.

think: Bogdan, a to pierwsze zadanie jest dobrze przepisane? Może ja coś już nie kumam, ale tam jest

sin2x		cos23x
	−		a to przecież
sin2x		cos2x

	cos3x
1 − (		)2 a to zawsze ≠ 4
	cosx

Bogdan: think, zadanie 7 jest dobrze rozwiązane, w zadaniu pierwszym w liczniku pierwszego ułamka powinno być sin²3x.

	sin23x		cos23x
zad 1.		−		= 4
	sin2x		cos2x

Dziękuję think za zauważenie

Godzio: zad. 2

	cos2x
cosx + sinx =
	1 − sin2x

sin2x ≠ 1

	π
2x ≠		+ 2kπ
	2

	π
x ≠		+ kπ
	4

(cosx + sinx)(1 − sin2x) = cos2x (cosx + sinx)(1 − sin2x) − (cosx − sinx)(cosx + sinx) = 0 (cosx + sinx)(1 − sin2x − cosx + sinx) = 0 cosx + sinx = 0 v 1 − 2sinxcosx − cosx + sinx = 0 sin²x + cos²x − 2sinxcosx − cosx + sinx = 0 sinx = t t² + t(1 − 2cosx) + cos²x − cosx = 0 Δ = 1 − 4cosx + 4cos²x − 4cos²x + 4cosx = 1 √Δ = 1

	−1 + 2cosx + 1
t1 =		= cosx
	2

	−1 + 2cosx − 1
t2 =		= cosx − 1
	2

cosx = sinx cosx − 1 = sinx

	π
cosx − cos(		− x) = 1
	2

	π   x + − x   2		π   x − + x   2
−2sin		sin		= 1
	2		2

	π		π		1
sin		*sin(x −		) = −
	4		4		2

√2		π		1
	*sin(x −		) = −
2		4		2

	π		√2
sin(x −		) = −
	4		2

	π
1)cosx = − sinx ⇒ cosx = cos(		+ x)
	2

	π
2)cosx = sinx ⇒ cosx = cos(		− x)
	2

	π		√2
3)sin(x −		) = −
	4		2

	π		π		π
1) x =		+ x + 2kπ v x = −		− x + 2kπ ⇒ x = −		+ kπ
	2		2		4

	π		π		π
2) x =		− x +2kπ v x = −		+ x + 2kπ ⇒ x =		+ kπ ∉ D
	2		2		4

	π		π		π		5π
3) x −		= −		+ 2kπ v x −		=		+ 2kπ
	4		4		4		4

	3π
x = 2kπ v x =		+ 2kπ
	2

	3π		π
Odp: x = 2kπ v x =		+ 2kπ v x = −		+ kπ
	2		4

Godzio: zad 1. sinx ≠ 0, cosx ≠ 0

	π		π
x ≠ kπ i x ≠		+ 2kπ i x ≠ −		+ 2kπ
	2		2

sin23x		cos23x
	−		= 4
sin2x		cos2x

(3sinx − 4sin3x)2		(4cos3x − 3cosx)2
	−		= 4
sin2x		cos2x

(3 − 4sin²x)² − (4cos²x − 3)² = 4 (3 − 4sin²x − 4cos²x + 3)(3 − 4sin²x + 4cos²x − 3) = 4 (3 − 4(sin²x + cos²x) + 3)(−4(sin²x − cos²x)) = 4 −2(sin²x − cos²x) = 1 2cos2x = 1

	1
cos2x =
	2

	π		π
2x =		+ 2kπ v 2x = −		+ 2kπ
	6		6

	π		π
x =		+ kπ v x = −		+ kπ
	12		12

	π		π
Odp: x =		+ kπ v x = −		+ kπ
	12		12

think: w takim razie pokuszę się o zrobienie pierwszego:

sin23x		cos23x
	−		= 4
sin2x		cos2x

	sin3x		cos3x
(		)2 − (		)2 = 4
	sinx		cosx

	sin3x		cos3x		sin3x		cos3x
(		−		)(		+		) = 4
	sinx		cosx		sinx		cosx

sin3x = 3sinxcos²x − sin³x cos3x = cos³x − 3sin²xcosx (3cos²x − sin²x − cos²x + 3sin²x)(3cos²x − sin²x + cos²x − 3sin²x) = 4 (2cos²x + 2sin²x)(4cos²x − 4sin²x) = 4 / : 2 4cos2x = 2 / :4

	1
cos2x =
	2

	π		π
2x =		+ 2kπ lub 2x = −		+ 2kπ, dla k∊Z
	3		3

	π		π
x =		+ kπ lub x = −		+ kπ
	6		6

	π		2
rozwiązaniem jest x =		+		kπ
	6		6

think: taaa Godzio ja wiem, że to Twój ukochany materiał....

Bogdan: think i Godzio − różne wyniki otrzymaliście w zadaniu1. Nie zobowiązująca uwaga. Sugeruję zapis k*2π, a nie 2kπ, k jest liczbą całkowitą, a zapis 2π określa długość okresu. W zapisie 2kπ nie widać wprost długości okresu. Podobnie

	1		1		1
w analogicznych zapisach: k*		π (okres ma długość		π), a nie		kπ.
	3		3		3

Godzio:

	π
TO ja się walnąłem bo coś mi się pokićkało że		to 60o co innego się myśli a co
	6

innego pisze

think: z.4. Cóż, albo coś sknociłam, albo .... log_kx, log_mx, log_nx ← postęp arytmetyczny log_kx + log_nx − 2log_mx = 0

logkx		logkx
	+ logkx − 2		= 0
logkn		logkm

	1		2
logkx(		+ 1 −		) = 0 ponieważ logkx ≠ 0, to
	logkn		logkm

1		2
	+ 1 −		= 0 / *logkn
logkn		logkm

	2logkn
1 + logkn −		= 0
	logkm

1 + log_kn = 2log_mn log_kkn = log_mn² n² = m^log_kkn

Bogdan: Zadanie 1. Można też tak, pokazuję początek rozwiązania:

sin23x		cos23x
	−		= 4
sin2x		cos2x

	π		π
Założenia: x ≠ kπ i x ≠		+ kπ ⇒ x ≠ k*
	2		2

	sin3x		cos3x		sin3x		cos3x
(		+		) (		−		) = 4
	sinx		cosx		sinx		cosx

(sin3x cosx + cos3x sinx) (sin3x cosx − cos3x sinx)
	= 4
sin2x cos2x

sin(3x + x) sin(3x − x) = 4sin²x cos²x sin4x sin2x = (sin2x)² sin4x sin2x − sin2x sin2x = 0 ⇒ sin2x (sin4x − sin2x) = 0 sin2x = 0 lub sin4x = sin2x itd.

think: Zgadza się Bogdan, różne, bo Godzio się już przy samych wynikach pomylił. Co do zapisu, to słuszna uwaga, po prostu nikt wcześniej nie zwrócił mi na to uwagi... no chyba, że nie pamiętam dokładnie lekcji w liceum, co też jest możliwe.

Eta: Dobry wieczór Widzę,że się spóźniłam, bo połowa zadań roztrzaskana A co z pozostałymi? zad5/ założenia x≥0 i y≥0 ( widzę na "oko" ,że x=y=4 wykazuję: 1/ p{x]+√y=4 |² x+y +2√xy= 16 2/ √x²+y²+√2*√xy= 8√2 \ * (−√2) −√2(x²+y²) − 2√xy= −16 równania 1) i 2) dodaję stronami i otrzymuję: √2(x²+y²)= x+y |² 2x²+2y² = x²+y²+2xy ( x−y)²=0 => x=y to: z 1) 2x+2x= 16 => x=4 to x=y=4 odp: rozwiazaniem układu jest : x=4 i y=4

Eta: zad8/ sin⁴x + cos⁴x= ³₄ ( sin²x+cos²x)²−2sin²x*cos²x= ³₄ Godzio ....... dokończ ..........

Bogdan: Dobry wieczór Eto, jeszcze trochę zadań zostało. W zadaniu 5 oczywiście x = y = 4

think: Eta a czy w zadaniu 5 nie może być rozwiązaniem np para (x,y) = (3, 11 +/− 4√2)

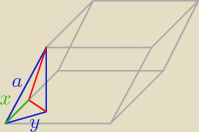
Godzio: zad. 3

	x
cosα =
	a

x = cosα * a

	1		x
cos		α =
	2		y

	x		cosα * a
y =		=
	1   cos α   2		1   cos α   2

H² + y² = a²

	cos2α*a2
H2 = a2 −
	1   cos2 α   2

	cos212α − cos2α
H = a√
	cos212α

	cos212α − cos2α
V = a2*sinα * H = a3 *√		* sinα
	cos212α

	cos212α − cos2α
(		) * sin2α =
	cos212α

	1 − sin212α − (1 − 2sin212α)2
4 *		* sin212cos212 =
	cos212α

4sin²¹₂α(1 − sin²¹₂α − 1 + 4sin²¹₂α − 4sin⁴¹₂α) = 4sin²¹₂α(3sin²¹₂α − 4sin⁴¹₂α) = 4sin³¹₂α(3sin¹₂α − 4sin³¹₂α) = 4sin³¹₂α*sin³₂α Odp: V = 2a³√sin³¹₂α*sin³₂α Ufff jakoś dobrnąłem do końca , mam nadzieje że dobrze

think: dobra zaczynam zadawać inteligentne pytania więc pora iść spać

Eta: zad. 10/ 1/ x*y=300 logarytmuję logarytmem dziesiętnym logx+logy= 2+log3 2/ podobnnie: logy*logx= 2log3 Godzio ....... dokończ odp: x= 3 x= 100 lub y= 100 y= 3 A teraz idę na herbatkę

Bogdan: Zadanie 3. Godzio − dobrze, można jeszcze ewentualnie wyłączyć przed pierwiastek

	α
sin
	2

think: ja idę spać, koniec weekendu jutro trzeba wcześnie wstać i w dodatku wykazać się jakąś przytomnością umysłu także i dziękuję za miły wieczór, życzę dobrej nocy i do następnego

Godzio: zad. 8 To kończę rozwiązanie Ety :

	3
( sin2x+cos2x)2−2sin2x*cos2x=
	4

	4sin2xcos2x		3
1 −		=
	2		4

	sin22x		1
−		= −
	2		4

	1
sin22x=
	2

	√2		√2
sin2x =		v sin2x = −
	2		2

	π		3		π		5
2x =		+ 2kπ v 2x =		π + 2kπ v 2x = −		+ 2kπ v 2x =		π + 2kπ
	4		4		4		4

	π		3		π		5
x =		+ kπ v x =		π + kπ v x = −		+ kπ v =		π + kπ
	8		8		8		8

	π		3		π		5
Odp: x =		+ kπ v x =		π + kπ v x = −		+ kπ v =		π + kπ
	8		8		8		8

Nie mam już sił myśleć czy da się to jakoś skrócić

Bogdan: pa, pa think

Godzio: Dobranoc think również idę po herbatkę i dalej robię zadanka − są naprawdę fajne

Eta: Dla think na dobranoc

Godzio: Jako "dokańczacz" dokończę 10 zad. 10 logx + logy = 2 + log3 x^logy = x^log_x9 logy = log_x9

	log9
logy =
	logx

logylogx = log9 logx = 2 + log3 − logy logy(2 + log3 − logy) = log9 2logy + logylog3 − log²y = log9 log²y − logy(2 + log3) + log9 t² − t(2 + log3) + log9 Δ = 4 + 4log3 + log²3 − 8log3 = log²3 − 4log3 + 4 = (log3 − 2)² √Δ = 2 − log3

	2 + log3 + 2 − log3
t1 =		= 2
	2

	2 + log3 − 2 + log3
t2 =		= log3
	2

logy = 2 logy = log100 y = 100 ⇒ x = 3 logy = log3 ⇒ y = 3 ⇒ x = 100 Nie wiedziałem czy o takie dokończenie chodziło ale dobra tam

Godzio: Podsumowując zrobione zadania są: 1,2,3,4,5,8,10 − napisałem żeby się nie mieszało

Godzio: zad 6. cos4x ≠ 0

	π		1		π		1
x ≠		+		kπ i x ≠ −		+		kπ
	8		2		8		2

	2tgα
tg4x = sin8x −− korzystam ze wzoru: sin2α =
	1 + tg2α

	2tg4x
tg4x =		−−− tg4x = t
	1 + tg24x

	2t
t =
	1 + t2

t(1 + t²) − 2t = 0 t(t² − 1) = 0 t(t − 1)(t + 1) = 0 t = 0 v t = 1 v t = −1

	π		π
x = kπ v x =		+ kπ v x = −		+ kπ
	4		4

	π		π
Odp: x = kπ v x =		+ kπ v x = −		+ kπ
	4		4

Godzio: 7 też zrobiona bo nie dopatrzyłem

Godzio:

	180		360		1
cos		* cos		=
	5		5		4

sin144 = sin(180 − 36) = sin36

	2sin36cos36*cos72		2sin72cos72
L = cos36 * cos72 =		=		=
	2sin36		4sin36

sin144		1
	=		= P
4sin36		4

Godzio: I w ten sposób poszły wszystkie zadanka

Bogdan: Zadanie 6 Godzio − popraw odpowiedzi

Godzio: poprawka do 6.

	kπ		π		kπ		π		kπ
Odp: x =		v x =		+		v x = −		+
	4		16		4		16		4

Bogdan: Teraz dobrze zad. 6, k piszemy nie w liczniku

	π		π		π		π		π
x = k*		lub x =		+ k*		lub x = −		+ k*
	4		16		4		16		4

Mam nadzieję Godzio, że nie przyjąłeś tej uwagi jako czepianie się drobiazgów, jestem za dbałością o elegancję zapisów

Bogdan: Do zadań ze starych arkuszy egzaminacyjnych jeszcze wrócimy, a teraz lulu, dobranoc

Godzio: Nie no, jasne że nie chętnie będę słuch wszelakich porad dotyczących matematyki

Godzio: ok Dobranoc