Zadania maturalne
AS: Oto zadania maturalne sprzed 80 lat
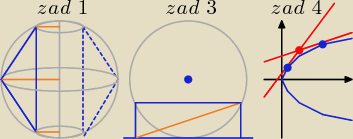
Zad 1. (1932 r)
W półkolu wystawionym na średnicy AB = 2R = 30.72 m
poprowadzono cięciwę CD równoległą do AB.
Łuk CD = 2α = 72o36' przepołowiono w punkcie E
i poprowadzono cięciwy EC i ED.
Znaleźć objętość bryły powstałej z obrotu trójkąta CED
dokoła średnicy AB.
Zad. 2
Trzy liczby dodatnie tworzą postęp geometryczny.Jeżeli do
drugiej liczby dodać 3,to postęp zamieni się na arytmetyczny.
Jeżeli do trzeciego wyrazu nowego postępu dodać 54,to
utworzy się znów postęp geometryczny. Znaleźć te liczby.
Zad.3
W kole o promieniu r poprowadzono styczną MN i równoległą
do niej cięciwę AB;rzut cięciwy na styczną oznaczono przez A'B'.
a) Wyrazić przekątną prostokąta ABB'A' jako funkcję odległości
cięciwy od stycznej.
b) Zbadać jak zmienia się długość przekątnej,gdy zmienia się
odległość cięciwy od stycznej.
Zad. 4
Z punktu A(12,9) poprowadzono styczne do paraboli y2 = 6x.
Wyznaczyć równanie okręgu,przechodzącego przez punkty
styczności i wierzchołek paraboli.
Zad.5
Parabola y = x2 − 5x + m jest styczna do osi x−ów i do prostej
y = 2x − n.Wyznaczyć punkt styczności paraboli z prostą.
15 sie 09:27
xxx: z.5 Skoro prosta o współczynniku kierunkowym a=2 jest styczna do paraboli, to znaczy, że
pochodna paraboli dla współrzędnej x musi być równa 2.Obliczamy pochodną funkcji kwadratowej
| | 7 | |
y'=2x−5 i przyrównujemy do 2. 2=2x−5 x= |
| , skoro parabola jest styczna do osi x−ów, to ma |
| | 2 | |
| | 25 | |
dokładnie jedno miejsce zerowe, zatem Δ=0 25−4m=0 obliczamy m= |
| , zatem parabola ma |
| | 4 | |
| | 25 | | 7 | |
równanie y=x2−5x+ |
| , za x podstawiamy |
| i otrzymujemy |
| | 4 | | 2 | |
| | 49 | | 35 | | 25 | | 37 | | 35 | |
|
| − |
| + |
| = |
| − |
| =1, zatem punkt styczności paraboli z prostą ma |
| | 4 | | 2 | | 4 | | 2 | | 2 | |
15 sie 13:44
think: zad2.
a, b, c ← geometryczny ⇒
b2 =
ac
a, b + 3, c ← arytmetyczny ⇒ 2(
b + 3) = a + c
a, b + 3, c + 54 ← geometryczny ⇒ (b + 3)
2 = a(c + 54) ⇒
ac = (b + 3)
2 − 54a
b
2 = (b + 3)
2 − 54a
b = 9a − 1,5
2(9a − 1,5 + 3) = a + c ⇒
c = 17a + 3
(9a − 1,5)
2 = a(17a + 3)
Δ = 900 − 576 = 324 = 4*81
√Δ = 2*9 = 18
| | 30 + 18 | | 3 | | 15 | | 75 | |
a1 = |
| = |
| ⇒ b1 = |
| i c1 = |
| |
| | 128 | | 8 | | 8 | | 8 | |
| | 30 − 18 | | 3 | | 27 | |
a2 = |
| = |
| ⇒ b2 = |
| − 1,5 < 0 odpada, bo a, b, c liczby |
| | 128 | | 32 | | 32 | |
dodatnie.
| | 3 | | 15 | | 75 | |
szukane liczby to : |
| , |
| , |
| . |
| | 8 | | 8 | | 8 | |
15 sie 14:07
think: to pierwsze to mi kosmiczne wychodzi, tym bardziej, że z całką, bo zdaje się w ten sposób
należy obliczyć objętość powstałej bryły. Także sobie daruje, pisanie do niego odpowiedzi,
może ktoś inny znajdzie na to jakiś zgrabny sposób...
15 sie 14:24
Bogdan:
Dzień dobry

Krótki komentarz do zadań.
1. Dzisiaj to zadanie mogłoby wystąpić na poziomie rozszerzonym, chociaż dane liczbowe
byłyby zapewne bardziej "gładkie", np. |AB| = 30, 2α = 120
o.
2. Standard z obecnego poziomu podstawowego.
3.Najciekawsze zadanie, szczególnie punkt b sprawiłby naszym maturzystom kłopot.
4. Nie omawia się obecnie parabol y
2 = ax, chociaż zadanie dość łatwe.
5. Zadanie z obecnego poziomu rozszerzonego (ze względu na parametry), dość łatwe.
Skąd
Asie wygrzebałeś ten zestaw? Sformułowanie: "W półkolu wystawionym na średnicy"
− cudeńko językowe. Pozdrawiam

15 sie 14:52
think:
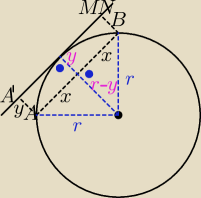
z.3
|A'A| = y ← to y opisuje nam odległość cięciwy od stycznej
|AB| = |A'B'| = 2x
a)y ∊ (0, 2r)
d − przekątna prostokąta AA'B'B
d
2 = y
2 + (2x)
2
x
2 + (r − y)
2 = r
2 ⇒ x
2 = 2ry − y
2
d
2 = y
2 +4(2ry − y
2) = −3y
2 + 8ry
d(y) = √8ry − 3y2
| | 8r − 6y | | 4 | |
b) d'(y) = (√8ry − 3y2)' = |
| = 0 ⇔ 8r − 6y = 0 ⇒ y = |
| r |
| | 2√8ry − 3y2 | | 3 | |
| | 4r | |
Dla y ∊ (0, |
| ) wraz ze wzrostem y, d rośnie. |
| | 3 | |
| | 4r | |
Dla y ∊ ( |
| , 2r) wraz ze wzrostem y, d maleje. |
| | 3 | |
15 sie 15:01
AS:
Zbiór zadań maturalnych Krawczyka wydany powielaczem ok. roku 1946.
15 sie 15:11
AS:
Zad.5
y = x
2 − 5*x + m
Parabola styczna do osi Ox,więc wierzchołek W(xw,0)
Wstawiając do równania paraboli mamy
| | 5 | | 5 | | 25 | |
0 = ( |
| )2 − 5* |
| + m ⇒ m = |
| |
| | 2 | | 2 | | 4 | |
| | 25 | |
Równanie paraboli: y = x2 − 5*x + |
| |
| | 4 | |
Prosta ma być styczna do praboli
| | 25 | |
x2 − 5*x + |
| = 2*x − n |*4 |
| | 4 | |
4*x
2 − 20*x + 25 = 8*x − 4*n
4*x
2 − 28*x + 25 + 4*n = 0
Warunek styczności: Δ = 0
Δ = (−28)
2 − 16*(25 + 4*n) = 0 ⇒ n = 6
Równanie prostej: y = 2*x − 6
Podstawiając n do równania i rozwiązując znajdziemy
| | 7 | |
punkt styczności S( |
| ,1)] |
| | 2 | |
15 sie 15:40
Radosław 2:
Zad 3
Poszukiwana funkcja: p=√8dr−3d2 p−przekątna d−odległość cięciwy od stycznej
Funkcja ta rośnie dla d∊(0;43r>
Czuwaj Asie i podaj czy to dobra odpowiedź
15 sie 15:42
AS:
| | 1 | |
Zgadza się. |
| matury zdałeś,bo na maturze dawano trzy |
| | 3 | |
zadania do rozwiązania.
15 sie 15:47
think: coś mi się zdaje, że z tego zestawu najrzadziej rozwiązywano zadanie 1, najczęściej
rozwiązywano 2 i 5 a później następował podział na to co komu leżało bardziej czy zadanie 3
czy 4...

no w każdym razie gdybym ja dostała taki zestaw na maturze, to pierwsze bym sobie
odpuściła chociażby ze względu na te okrągłe liczby

15 sie 16:34
AS: Odpowiedzi
Zad 2. 3/8 , 15/8 , 75/8
Zad 3. y2 = −3*x2 + 8*R*x , ymax przy x = 4*R/3
Zad 4. (x − 24)2 + (y + 18)2 = 200
Zad. 5 S(7/2,1)
15 sie 17:49
think: AS a co z odpowiedzią do 1?
15 sie 17:51
think: jestem ciekawa czy ten moloch którego liczyłam był dobrze.
15 sie 17:51
AS: Moje obliczenia do zad. 1 − ale jeszcze raz sprawdzę
| | 2*π | |
V = |
| *R3*cosα(cos2α + sinαcosα − 2*sin2α) |
| | 3 | |
15 sie 18:03
Bogdan:
Uwaga do zadania 1. Wyprowadzona zależność na V musi być w postaci logarytmicznej,
takie wymóg wówczas obowiązywał.
15 sie 18:13
AS: Każda reguła na swoje wyjątki − tu nie da się sprowadzić
do postaci logarytmicznej.
15 sie 18:30
think: hmm ja oczywiście pierwotnie powstawiałam tam wszystkie liczby, oczywiście głupio zrobiłam,
teraz to spokojnie przeliczyłam operując symbolami i wyszło mi ciut inaczej.
| | 2πR3 | |
V = |
| sinα(cosα − cos2α) |
| | 3 | |
15 sie 18:36
think: Bogdan ja nie wiem jaka to postać logarytmiczna, podaj przykład proszę.
15 sie 18:36
Bogdan:
Weźmy wzór wyprowadzony przez
Asa.
| | 2π | |
V = |
| * r3 * cosα * (cos2α + sinαcosα − 2*sin2α) |
| | 3 | |
Ten wzór zawiera wyrażenie: cos
2α + sinαcosα − 2*sin
2α, którego nie można zostawić
w postaci sumy, trzeba przekształcić do postaci iloczynowej, którą nazywamy postacią
logarytmiczną, bo po wstawieniu wartości liczbowych łatwo wyznacza się wynik stosując
logarytmy.
Nie ma wyjątków, każde wyrażenie można doprowadzić do postaci logarytmicznej, to była
zresztą największa bolączka ówczesnych uczniów i studentów.
Pokażę to na omawianym przykładzie.
cos
2α + sinαcosα − 2*sin
2α = −cos
2α(2tg
2α − tgα − 1) =
| | 1 | |
= −cos2α * 2(tgα + |
| ) (tgα − 1) = |
| | 2 | |
= −2cos
2α * (tgα + tg26
o34') (tgα − tg45
o) =
| | sin(α + 26o34') | | sin(α − 45o) | |
= −2cos2α * |
| * |
| = |
| | cosα cos26o34' | | cosα cos45o | |
| | −2sin(α + 26o34') sin(α − 45o) | | √2 | |
= |
| * |
| = |
| | | | √2 | |
| | −2√2 sin(α + 26o34') sin(α − 45o) | |
= |
| |
| | cos245o | |
To jest wyrażenie w postaci logarytmicznej.
Dodam, że szczytem szpanu była wtedy umiejętność wykonywania skomplikowanych obliczeń
rachunkowych przy pomocy suwaka logarytmicznego. Podkreślam, że obliczenia były możliwe
tylko po doprowadzeniu wyrażenia do postaci logarytmicznej.
15 sie 19:08
Bogdan:
Zgubiłem w mianowniku cos26o34'
15 sie 19:10
Bogdan:
Poprawiam dwie ostatnie linijki:
| | −2sin(α + 26o34') sin(α − 45o) | | √2 | |
... = |
| * |
| = |
| | | | √2 | |
| | −2√2 sin(α + 26o34') sin(α − 45o) | |
= |
| |
| | cos26o34' | |
15 sie 19:16
AS: Górą Bogdan!
Nie pomyślałem o rozkładzie na iloczyn.
Wszelakiej pomyślności.
15 sie 19:16
Bogdan:

15 sie 19:16
think: 
dziękuję, teraz już będę wiedziała jak to wyglądało. Pełen podziw dla uczniów tamtych
czasów, troszkę żałuję, że już z innej 'epoki' matematyki się wywodzę.
15 sie 19:29
think: w moim byłoby to jeszcze prostsze, z różnicy cosinusów..., tylko nie wiem czy moje jest
poprawnie...
15 sie 21:27
Włodek: cos26o34 co to jest MATEMATYCY;>?
29 lut 16:01
przerażony krejzol: chyba bym nie zdał ale w 2012 mam 100%
10 maj 22:51
czekoladowe sny: to zad 2 było w tym roku na rozsz tylko z innymi liczbami
10 maj 22:55
Mila: I wszyscy znali grekę, łacinę i nowożytny język! Moi wujowie recytowali mi dzieła starożytnych
poetów, a także fragmenty pamiętników Cezara.
10 maj 22:57
KacpeR: przerazony krejzol, bys nie zdal ale w tym roku masz 100%? smieszne .. skoro masz 100% to bys
zrobil na spokojnie 3 zadania stad
10 maj 22:57
Nienor: A ile trzeba było mieć żeby zdać?
11 maj 17:38
antoni:
9 wrz 20:56
 Dzień dobry
Dzień dobry  Krótki komentarz do zadań.
1. Dzisiaj to zadanie mogłoby wystąpić na poziomie rozszerzonym, chociaż dane liczbowe
byłyby zapewne bardziej "gładkie", np. |AB| = 30, 2α = 120o.
2. Standard z obecnego poziomu podstawowego.
3.Najciekawsze zadanie, szczególnie punkt b sprawiłby naszym maturzystom kłopot.
4. Nie omawia się obecnie parabol y2 = ax, chociaż zadanie dość łatwe.
5. Zadanie z obecnego poziomu rozszerzonego (ze względu na parametry), dość łatwe.
Skąd Asie wygrzebałeś ten zestaw? Sformułowanie: "W półkolu wystawionym na średnicy"
− cudeńko językowe. Pozdrawiam
Krótki komentarz do zadań.
1. Dzisiaj to zadanie mogłoby wystąpić na poziomie rozszerzonym, chociaż dane liczbowe
byłyby zapewne bardziej "gładkie", np. |AB| = 30, 2α = 120o.
2. Standard z obecnego poziomu podstawowego.
3.Najciekawsze zadanie, szczególnie punkt b sprawiłby naszym maturzystom kłopot.
4. Nie omawia się obecnie parabol y2 = ax, chociaż zadanie dość łatwe.
5. Zadanie z obecnego poziomu rozszerzonego (ze względu na parametry), dość łatwe.
Skąd Asie wygrzebałeś ten zestaw? Sformułowanie: "W półkolu wystawionym na średnicy"
− cudeńko językowe. Pozdrawiam 
 z.3
|A'A| = y ← to y opisuje nam odległość cięciwy od stycznej
|AB| = |A'B'| = 2x
a)y ∊ (0, 2r)
d − przekątna prostokąta AA'B'B
d2 = y2 + (2x)2
x2 + (r − y)2 = r2 ⇒ x2 = 2ry − y2
d2 = y2 +4(2ry − y2) = −3y2 + 8ry
d(y) = √8ry − 3y2
z.3
|A'A| = y ← to y opisuje nam odległość cięciwy od stycznej
|AB| = |A'B'| = 2x
a)y ∊ (0, 2r)
d − przekątna prostokąta AA'B'B
d2 = y2 + (2x)2
x2 + (r − y)2 = r2 ⇒ x2 = 2ry − y2
d2 = y2 +4(2ry − y2) = −3y2 + 8ry
d(y) = √8ry − 3y2
 no w każdym razie gdybym ja dostała taki zestaw na maturze, to pierwsze bym sobie
odpuściła chociażby ze względu na te okrągłe liczby
no w każdym razie gdybym ja dostała taki zestaw na maturze, to pierwsze bym sobie
odpuściła chociażby ze względu na te okrągłe liczby

 dziękuję, teraz już będę wiedziała jak to wyglądało. Pełen podziw dla uczniów tamtych
czasów, troszkę żałuję, że już z innej 'epoki' matematyki się wywodzę.
dziękuję, teraz już będę wiedziała jak to wyglądało. Pełen podziw dla uczniów tamtych
czasów, troszkę żałuję, że już z innej 'epoki' matematyki się wywodzę.