Matura z 1960 r.
Bogdan:
Przedstawiam zestaw maturalny sprzed pół wieku, z 1960 r. z Wrocławia.
Zestaw zawiera 3 zadania, nie było wtedy kalkulatorów, można było skorzystać z tablic
logarytmicznych i z tablic funkcji trygonometrycznych. Wzory trzeba było znać.
Zachowuję oryginalne sformułowania, określenie "postęp" oznacza ciąg.
1. Krawędź podstawy graniastosłupa prawidłowego trójkątnego wynosi a. Dwa wierzchołki
górnej podstawy połączono ze środkami przeciwległych krawędzi dolnej podstawy.
Wyznaczyć objętość tego graniastosłupa, wiedząc, że kąt miedzy otrzymanymi odcinkami
wynosi α.
Wykonać obliczenia dla a = 14,09 dm, α = 26o48'.
2. Znaleźć cztery liczby, z których trzy pierwsze tworzą postęp geometryczny, trzy ostatnie
zaś tworzą postęp arytmetyczny. Suma liczb pierwszej i czwartej jest 14, suma drugiej
i trzeciej równa się 12.
3. Wykreślić równoległobok wiedząc, że jego kąt ostry wynosi α, a odległości punktu przecięcia
się przekątnych tego równoległoboku od dwóch różnych boków równe są odpowiednio a i b.
Wyznaczyć pole tego równoległoboku.
14 sie 22:52
Godzio:
2.
a,b,c,d
a,b,c −− ciąg geometryczny: b
2 = a * c
b,c,d −− ciąg arytmetyczny: 2c = b + d
a + d = 14
b + c = 12 + ⇒ c = 12 − b
−−−−−−−−−−−−−−
b + d = 26 − a − c
2c = 26 − a − c ⇒ a = 26 − 3c ⇒ a = 26 − 36 + 3b ⇒ a = −10 + 3b
b
2 = (3b − 10)(12 − b)
b
2 = 36b − 3b
2 − 120 + 10b
4b
2 − 46b + 120 = 0
2b
2 − 23b + 60 = 0
Δ = 529 − 8 * 60 = 529 − 480 = 49
√Δ = 7
| | 23 + 7 | | 15 | |
b1 = |
| = |
| = 7,5 |
| | 4 | | 2 | |
Odp:
1
o b = 7,5 ⇒ c = 4,5, a = 12,5, d = 1,5
2
o b = 4 ⇒ c = 8, a = 2, d = 12
14 sie 23:41
15 sie 00:41
Godzio:
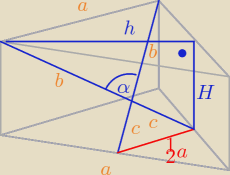
1.
a
2 = 2b
2 − 2b
2cosα
H
2 + h
2 = (b + c)
2
| | 3 | | | | | | | |
H2 + |
| a2 = |
| + |
| + |
| |
| | 4 | | 1 − cosα | | 1 − cosα | | 1 − cosα | |
| | 4,5a2 − 3a2(1 − cosα) | |
H2 = |
| |
| | 4 − 4cosα | |
| | a2(1,5 + 3cosα) | |
H2 = |
| |
| | 4 − 4cosα | |
H = U{a
√1,5 + 3cosα}{2
√1 − cosα
| | a2√3 | | a√1,5 + 3cosα | |
V = |
| * |
| |
| | 4 | | 2√1 − cosα | |
| | 3a3√0,5 + cosα | |
V = |
| |
| | 8√1 − cosα | |
a = 14,09 dm, α = 26
o48'
cos(26
o48') ≈ 0,659
| | 3(14,09)3√0,5 + 0,659 | | 8391,782787 * √0,3295 | |
V = |
| = |
| = |
| | 8√1 − 0,659 | | 8√0,341 | |
= 1031,133192 ≈ 1031,13 dm
3
15 sie 00:47
Godzio:
heh, do tamtego to tak nie ma co brawa bić bo nie było zbyt trudne, jestem ciekaw czy to mam
dobrze

15 sie 00:48
Jaga:
2) sposób:
a,b,c,d −−− szukane liczby
z własności postępu arytm.
c= b+r d= b+2r
z układu równań a+d=14 i b+c= 12
b = 6−
r2 a= 8−
32r c= 6+
r2 d= 6+
32r
z własności postępu geom.: b
2=a*c
otrzymamy: r
2−r−12=0
to r= 4 v r= −3
szukane liczby:
1
o : 2, 4,8,12
2
o : 12,5 ; 7,5; 4,5; 1,5

15 sie 00:54
Bogdan:
Mam nadzieję Godzio, że nie używałeś kalkulatora. Zadanie nr 2 jest dobrze rozwiązane,
zadanie nr 1 − nie.
15 sie 00:57
Godzio:
Dobra to w takim razie jeszcze pomyślę a kalkulator to tylko do 2 w obliczaniu V po
podstawieniu

ale skoro i tak źle to kicha
15 sie 00:59
Godzio:
Bogdan a możesz zdradzić czy rysunek dobrze zrobiłem ?
15 sie 01:00
Bogdan:
Do takich obliczeń nie używano kalkulatora, bo go wtedy jeszcze nie było, wykorzystywano
logarytmy. Nawet funkcjonowało wtedy sformułowanie "doprowadzić wyrażenie, do postaci
logarytmicznej", prawda Eto, Asie, Basiu i wszyscy, którzy pamiętają tamte
czasy?
15 sie 01:07
Bogdan:
Rysunek jest dobrze, pokaż jednak inne h (h to wysokość trójkąta równobocznego
będącego podstawą graniastosłupa).
15 sie 01:10
Bogdan:
Dodam, że wtedy matematyka była obowiązkowa, nie było poziomu podstawowego
i rozszerzonego, wszystkie wzory trzeba było znać, arkusze nie były drukowane,
zadania były zapisane kredą na tablicy. Proszę zauważyć, jak ma się poziom wymagań
sprzed pół wieku do tego, który obowiązuje obecnie, a z którym i tak wielu sobie nie
radzi. Jest więc postęp, czy nie?

15 sie 01:22
Godzio:
No wiadomo że nie, teraz to coraz mniejszy poziom, a szkoda ...
15 sie 01:29
Bogdan:
Obowiązywały wtedy i jeszcze przez wiele następnych lat, egzaminy do uczelni wyższych.
Poziom zadań egzaminacyjnych był wyższy od poziomu zadań maturalnych. Pokażę
w ciągu dnia w oddzielnym poście kilka takich zadań, teraz czas na sen. Dobranoc

15 sie 01:36
Godzio:
No to w takim razie czekam, w tym zadaniu nie mam pojęcia w czym rzecz

, widocznie nie
dostrzegam błędu no ale dobra jeszcze pomyślę.
Dobranoc

15 sie 01:39
Eta:
Witam
Bogdanie 
Omg .... matura 1960 ? ( byłam wtedy jeszcze w podstawówce

Za kilka lat była moja matura, pamiętam te wszystkie zadania ze stereometrii
kończące się : " sprowadź do postaci logarytmicznej"
i wykonaj obliczenia dla .......
Pamiętam do dzisiaj niektóre mantysy logarytmów:
np: 0, 3010 ; 0, 4771
To były czasy...... nie to co teraz,gdzie wszystko gotowe na tacy
net, Wikipedia,
matematyka . pisz 
A mimo to efekty są takie jak widać często na naszym forum.
Wzory znaliśmy na zawołanie ( i wyprowadzenia tych wzorów też, gdy zachodziła taka
potrzeba)
jakoś pomieściły się w naszych głowach i zostały zakodowane do dzisiaj
i nie uważam,że "zasmieciły" mi mózg

Tak
Godzio , tak to było .....

Pozdrawiam

15 sie 02:03
Eta:
Miłych snów, dobranoc

15 sie 02:05
Bogdan:
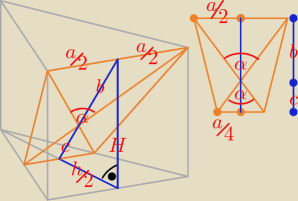
Szkic rozwiązania zadania 1.
| | 1 | |
Objętość V = |
| a2*H, H = √ (b + c)2 − (h/2)2 |
| | 4 | |
| h | | 1 | | a√3 | | a√3 | | h | | 3 | |
| = |
| * |
| = |
| , ( |
| )2 = |
| a2 |
| 2 | | 2 | | 2 | | 4 | | 2 | | 16 | |
| b | | α | | a | | α | |
| = ctg |
| ⇒ b = |
| ctg |
| |
| | 2 | | 2 | | 2 | |
| c | | α | | a | | α | |
| = ctg |
| ⇒ b = |
| ctg |
| |
| | 2 | | 4 | | 2 | |
| | 3 | | α | | 9 | | α | |
b + c = |
| a ctg |
| , (b + c)2 = |
| a2 ctg2 |
| , |
| | 4 | | 2 | | 16 | | 2 | |
| | 1 | |
H = √ (b + c)2 − (h/2)2 = |
| a √3 √ 3ctg2(α/2) − 1 |
| | 4 | |
| | 1 | | 3 | | 3 | |
V = |
| a2*H = |
| a3 √ 3ctg2(α/2) − 1 = |
| a3 √ w |
| | 4 | | 16 | | 16 | |
(Komentarz: wzór na objętość V w takiej postaci nie zostałby uznany, należy doprowadzić
wyrażenie do postaci logarytmicznej, inaczej mówiąc − do postaci iloczynowej)
| | α | | √3 | | α | | √3 | |
w = 3ctg2(α/2) − 1 = 3 (ctg |
| − |
| ) (ctg |
| + |
| ) = |
| | 2 | | 3 | | 2 | | 3 | |
| | | | 1 | | 1 | | sin(60o − |
| ) sin(60o + |
| ) | | | 2 | | 2 | |
| |
= 3 * |
| = |
| | | |
| | | | 1 | | 1 | | sin(60o − |
| ) sin(60o + |
| ) | | | 2 | | 2 | |
| |
= 4 * |
| |
| | | |
| | 2 √ sin(60o − (1/2) ) * sin(60o + (1/2) ) | |
√ w = |
| |
| | | |
| | 3a3 √ sin(60o − (1/2) ) * sin(60o + (1/2) ) | |
= |
| |
| | | |
Po wstawieniu danych liczbowych otrzymujemy V = 3778 dm
3 z dokładnością do 1 dm
3.
15 sie 16:10
Godzio:
Bogdan nie wiem czemu ale nie widzę nic złego w moim rozwiązaniu, z tego co
przeanalizowałem w Twoim to:
| | cos(α − β) − cos(α + β) | |
Wykorzystam wzór: sinα*sinβ = |
| |
| | 2 | |
| | | | α | | α | | sin(60 − |
| )*sin(60 + |
| ) | | | 2 | | 2 | |
| |
w = ... = 3 * |
| = |
| | | |
| | | cos(60 − ( (α)/2) − 60 − ( (α)/2)) − cos(60 − ( (α)/2) + 60 + ( (α)/2)) | |
| | | 2 | |
| |
4 * |
| |
| | | |
=
| | cos(−α) − cos120 | | | |
4 * |
| = 4 * |
| = |
| | | | | |
| | 1 | | α | |
4 * |
| * U{cosα + 0,5}{sin2 |
| |
| | 2 | | 2 | |
Czyli ostatecznie:
| | 3 | | 3 | | √0,5 + cosα | |
V = |
| a3 * √w = |
| a3 * |
| |
| | 16 | | 8 | | | |
Teraz moje rozwiązanie:
| | 3a3 √0,5 + cosα | |
V = |
| |
| | 8√1 − cosα | |
| | α | | α | | α | | α | |
1 − cosα = 1 − (cos2 |
| − U{sin2 |
| ) = 1 − (1 − 2sin2 |
| ) = 2 sin2 |
| |
| | 2 | | 2 | | 2 | | 2 | |
Czyli doszedłem do tego że Twoje i moje rozwiązania są identyczne tyle że przedstawione w innej
formie, co o tym sądzisz ?
15 sie 18:02
Godzio:
Zapisze bardziej czytelniej:
| | | cos(60 − α/2 − (60 + α/2) ) − cos(60 − α/2 + 60 + α/2) | |
| | | 2 | |
| |
w = ... = 4 * |
| |
| | | |
=
15 sie 18:09
Bogdan:
Godzio − Twoj wzór na V nie byłby uznany, bo nie jest w postaci iloczynowej, nie może
być wyrażenie w postaci cosα + 0,5.
W pierwszym Twoim rozwiązaniu uzyskałeś wynik V = 1031,13, nie był to prawidłowy wynik.
15 sie 18:34
Godzio:
jeszcze raz sprawdziłem dokładnie na kalkulatorze i wyszło jednak 3777 wtedy chyba coś źle
napisałem i może stąd taki wynik, a co do rozwiązania to wychodzi na to że było poprawne
rozumowanie tylko końcowy zapis objętości powinienem zapisać w postaci iloczynowej
tzn w tym wypadku rozpisać dokładniej cosα + 0,5 ?
| | α + 60 | | α − 60 | |
cosα + cos60 = 2 * cos |
| * cos |
| |
| | 2 | | 2 | |
| | 3 | | √cosα + 602 * cosα − 602 | |
Odp: V = |
| a3 * |
| |
| | 8 | | | |
Czy taka odpowiedź byłaby już prawidłowa ?
15 sie 19:03
Szprot: Jak by takie były zadania na Maturze wtedy to nikt by ich nie zdawał

15 sie 19:22
Godzio:
Jak na maturze byłyby takie zadania to maturzyści musieliby być do takowej matury odpowiednio
przygotowani, kiedyś zdawali to teraz też by musieli

15 sie 19:24
Bogdan:
Wtedy były takie właśnie zadania i przystępowali do matury wszyscy, nie wszyscy jednak ją
zdawali, można było przystąpić do poprawki za rok.
| | α | | 1 | |
W ostatnim moim wyrażeniu na V zamiast |
| napisałem |
| , podaję więc jeszcze raz: |
| | 2 | | 2 | |
| | 3a3 √ sin(60o − (α/2) ) sin(60o + (α/2) ) | |
V = |
| |
| | | |
15 sie 19:45



 1.
1.


 ale skoro i tak źle to kicha
ale skoro i tak źle to kicha


 , widocznie nie
dostrzegam błędu no ale dobra jeszcze pomyślę.
Dobranoc
, widocznie nie
dostrzegam błędu no ale dobra jeszcze pomyślę.
Dobranoc 
 Omg .... matura 1960 ? ( byłam wtedy jeszcze w podstawówce
Omg .... matura 1960 ? ( byłam wtedy jeszcze w podstawówce  Za kilka lat była moja matura, pamiętam te wszystkie zadania ze stereometrii
kończące się : " sprowadź do postaci logarytmicznej"
i wykonaj obliczenia dla .......
Pamiętam do dzisiaj niektóre mantysy logarytmów:
np: 0, 3010 ; 0, 4771
To były czasy...... nie to co teraz,gdzie wszystko gotowe na tacy
net, Wikipedia, matematyka . pisz
Za kilka lat była moja matura, pamiętam te wszystkie zadania ze stereometrii
kończące się : " sprowadź do postaci logarytmicznej"
i wykonaj obliczenia dla .......
Pamiętam do dzisiaj niektóre mantysy logarytmów:
np: 0, 3010 ; 0, 4771
To były czasy...... nie to co teraz,gdzie wszystko gotowe na tacy
net, Wikipedia, matematyka . pisz  A mimo to efekty są takie jak widać często na naszym forum.
Wzory znaliśmy na zawołanie ( i wyprowadzenia tych wzorów też, gdy zachodziła taka
potrzeba)
jakoś pomieściły się w naszych głowach i zostały zakodowane do dzisiaj
i nie uważam,że "zasmieciły" mi mózg
A mimo to efekty są takie jak widać często na naszym forum.
Wzory znaliśmy na zawołanie ( i wyprowadzenia tych wzorów też, gdy zachodziła taka
potrzeba)
jakoś pomieściły się w naszych głowach i zostały zakodowane do dzisiaj
i nie uważam,że "zasmieciły" mi mózg  Tak Godzio , tak to było .....
Tak Godzio , tak to było .....  Pozdrawiam
Pozdrawiam 

 Szkic rozwiązania zadania 1.
Szkic rozwiązania zadania 1.

