Równania stycznych Handi: Wyznacz równania stycznych do elipsy o równaniu x²+4y²=4 przechodzących przez punkt A=(4,0).

Godzio: styczna: y = ax + b 0 = 4a + b b = −4a y = ax − 4a x² + 4(ax − 4a)² = 4 x² + 4(a²x² − 8a²x + 16a²) = 4 x²(1 + 4a²) −32a²x + 64a² − 4 = 0 Δ = 1024a⁴ − (4+16a²)(64a² − 4) = 1024a⁴ − 256a² + 16 − 1024a⁴ + 64a² = −192a² + 16 zał. Δ = 0 192a² = 16

	1
a2 =
	12

	√3		√3
a =		v a = −
	6		6

	−2√3		2√3
b = −4a =		v b =
	3		3

Równania stycznych:

	√3		2√3
y =		x −
	6		3

	√3		2√3
y = −		x +
	6		3

Handi: Czyli podobnie jak równania stycznych do okręgu...

Handi: Godzio a czemu delta musi być równa 0?

Godzio: Bo styczna ma jeden punkt wspólny z elipsą

Godzio: inaczej, jedno rozwiązanie daje nam tylko gdy Δ = 0 i wtedy mamy pewność że jest tylko jeden punkt wspólny

Handi: Ok dzięki

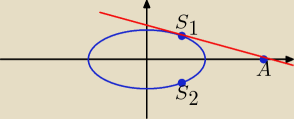
Bogdan: Rozwiązanie Godzia jest prawidłowe. Podaję inny sposób. S(x_S, y_S) − punkt elipsy, w którym prosta przechodząca przez punkt A(4, 0) jest do niej styczna. Wzór stycznej do elipsy x² + 4y² = 4 w punkcie S: x_Sx + 4y_Sy = 4. Do tej prostej należy punkt A(4, 0), a więc: x_s*4 + 4y_S*0 = 4 ⇒ 4x_S = 4 ⇒ x_S = 1 Punkt S nalezy do elipsy, możemy więc zapisać: x_S² + 4y_S² = 4 Wstawiamy x_S = 1:

	3		√3		√3
1 + 4yS2 = 4 ⇒ yS2 =		⇒ yS =		lub yS = −
	4		2		2

	√3		√3
Mamy 2 punkty styczności: S1 = (1,		) oraz S2 = (1, −		)
	2		2

Wystarczy teraz napisać równanie prostej zawierającej punkty A, S₁ oraz prostej zawierającej punkty A, S₂.

AS: Można też skorzystać z gotowego wzoru równania stycznej o danym kierunku m. Jest to powtórzenie rozwiązania podanego przez Godzio. Równanie stycznej y = m*x ± √a²*m² + b² Dla x = 4 , y = 0 mamy 0 = 4*m ± √4*m² + 1 4*m = ± √4*m² + 1 do kwadratu 16*m² = 4*m² + 1 12*m² = 1

	1
m = ±
	√12

m wstawić do podanego równania i po krzyku.