POMOCY Mariolaa: Godzio a ja mogę Cię poprosic o jakies zadania maturalne z trygonometrii?

Godzio: podstawa / rozszerzenie ?

damian: Co prawda nie jestem Godzio ale zadanie jest wg mnie warte uwagi: Wyznacz najmniejszą wartość

	(ctg2x−tg2x)*sin22x
funkcji f(x)=
	4cos2x*sin2x

Godzio: To wyrażenie w ogóle osiąga wartość najmniejszą?

Mariolaa: podstawowa

Bogdan: To wyrażenie posiada wartość najmniejszą.

Godzio: 1. Oblicz: a) (cos45 − cos30)(cos45 + cos30) b) 4(ctg45 + sin60)(cos30 + tg45) c) (sin45 + ctg45)(6 * sin60 − ctg30) 2. Oblicz pozostałe wartości funkcji trygonometrycznych wiedząc że: a) ctgx = 3 x ∊ (0,90)

	5
b) sinx =
	13

Tyle na początek

Mariolaa: 1) (√2przez 2 − √3 przez 2) (√2przez 2 + √3 przez 2) = (√2przez 2)² −(√3przez 2)²= 2 przez 4 − 3/4 = −1/4

Kejt: Mariolu. zapisuj to tak: U{...} {...} usuń tylko spację ze środka, a w miejsce kropek wpisz liczby. Wyjdzie Ci wtedy ułamek..

Mariolaa: 2) 4(1+ √3/2)(√3/2+1)=4(1+ √3/2)(1−√3/2)= 4(1)²−(√3/2)²= 4*1− 3/4= 5−3/4 =5/4

Mariolaa: dzięki uzyje tego w nastepnym zadaniu

Godzio: 2) coś Ci źle wyszło popraw zauważ że masz:

	√3		√3		√3
4(1 +		)(		+ 1) = 4(1 +		)2 = ...
	2		2		2

Godzio: a możesz jeszcze wciągnąć tą 4 do nawiasu

	√3
22 * (1 +		)2 = (2 + √3)2 = ...
	2

teraz to pikuś

Mariolaa: 2²+2*2*√3+√3²= 4+4√3+3=11√3

Mariolaa: a drugie zadanie mi wyszło po podstawieniu tg=¹₃, sin= ^√10₁₀ cos= ^13√10₁₀

Kejt: nie możesz tak dodać.. 4+3+4√3=7+4√3

Godzio:

	3√10
ok tylko przy cosx =
	10

Mariolaa: ad2.b sin ⁵₁₃ cos 12 tg ²²¹₁₅₆ ctg 14 sorrki ze tak pozno ale problem z internetem miałam

Godzio: nie ma problemu, ale chyba coś nie tak, pomyśl jeszcze

Mariolaa: a tego ad1.c nie wiem jak zrobic

Mariolaa: tzn która odp jest zła?

Mariolaa: a cos zle i i reszta zle powinno być ¹⁴⁴₁₆₉ tak?

Godzio: jeśli cos wyszedł Ci 12 to chyba coś nie tak prawda ?

Godzio:

	5
sinx =
	13

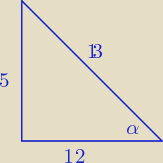
Sposób I : sin²x + cos²x = 1

25
	+ cos2x = 1
169

	144
cos2x =
	169

	12
cosx =
	13

	sinx		5		13		5
tgx =		=		*		=
	cosx		13		12		12

	12
ctgx =
	5

Sposób II −− rysunek

	5
zaznaczamy na rysunku α i zgodnie z danymi zaznaczamy boki sinα =
	13

x² + 5² = 13² x² = 144 x = 12 I tera już odczytujemy pokolei funcje

	12
cosα =
	13

	5
tgα =
	12

	12
ctgα =
	5

Mariolaa: ooo rany niby proste a ja się nie mogę zabrac za to

Godzio: pokazać 1. c) czy jeszcze walczysz ?

Mariolaa: taak taak zagalopowałam się troszke z tym cosinusem hehe

Mariolaa: probuje ale z moją błyskotliwością sądze ze mi nie wyjdzie hee

Godzio: To poczekamy jeszcze, podstaw poupraszczaj to co się da w nawiasach i na końcu przemnóż

Mariolaa: nie wychodzi. prosze o pomoc

Godzio:

	√2		√3		√2
(		+ 1)(6 *		− √3) = (		+ 1) * (3√3 − √3 ) =
	2		2		2

	√2
= (		+ 1) * 2√3 = √6 + 2√3
	2

Mariolaa: a ja kombinowałam jak podstawic do wzoru matematyka nie jest na moją głowe

Mariolaa: dasz mi jeszcze jakies przykłady czy masz dośc takich jak ja hihi

Godzio: Ważne że próbujesz To może teraz coś z tożsamości: 1. Sprawdź czy podane równości są tożsamościami, podaj założenia

	tgx
a)sinx *		= 1
	sinx

	ctgx
b)cosx + cosx * ctg2x =
	sinx

2. Zapisz wyrażenia w najprostszej postaci: a) (cosx + tgx * sinx) * ctgx

	1
b)		− cosx * ctgx
	sinx

3. Oblicz: a) sin²75 + sin²15 − 2sin30 −−− mam nadzieję że umiesz posługiwać się wzorami redukcyjnymi

Godzio: Mam dość leniów, a nie tych którzy chcą się czegoś nauczyć

Godzio: zad. 1

	tgx
a) powinno być cosx *
	sinx

Mariolaa: a tożsamości nie są na rozszerzonym?

Godzio: wracam za jakieś 20 min i sprawdzę Twoje rozwiązania

Godzio: być może ale to jak chcesz to zrób w takim razie 2 i 3 jeśli nie chcesz tożsamości

Mariolaa: 2) a cos*sin*tg*ctg² b 1−^cos*tg_sin

Mariolaa: https://matematykaszkolna.pl/strona/i16.html wzory też na rozszerzonym po kolorach poznaje

Godzio: tgx * ctgx = 1

	sinx
a) (cosx + tgx * sinx) * ctgx = cosx * ctgx + tgx * ctgx * sinx = cosx *		+
	cosx

sinx = sinx + sinx = 2sinx

Godzio: tak ale nie dla (90^o + α) i (90^o − α) −to jest na 100% na podstawie

Godzio:

	cosx		cos2x + sin2x		1
tak się pomyliłem cosx *		+ sinx =		=
	sinx		sinx		sinx

Godzio: nad b) pomyśl jeszcze

Mariolaa: a skąd Ci się wzięło cosx* ^sinx_cosx

Godzio:

	cosx
napisałem nieco wyżej ze mialo byc cosx*
	sinx

Mariolaa: pogmatwałam sie całkowicie pomyliłes sie w pierwszym a ja robiłam 2

Mariolaa: a tego 3 nie wiem jak rozgryzc

Godzio: sin²15 = sin²(90 − 75) = cos²75, a teraz ?

Mariolaa: kurcze ja w ogole nie wiem o co chodzi w tych wzorach

Godzio: a przerabiałaś w ogóle trygonometrię w szkole ?

Mariolaa: no tak

Godzio: i nie miałaś podstawowych wzorów redukcyjnych ?

Mariolaa: jeszcze specjalnie przeglądnęłam zeszyty bo swojej pamieci nie zawsze do konca ufam i nie miałam

Godzio: no to kicha a powinnaś to mieć

Mariolaa: porazka