oblicz Jaga: zad. dla Kejt Podaj wartość : 2−3+6−7+10 −11+ ........... + 2010 −2011.

think: a ja nie masz nic dla mnie?

Jaga: ....... za chwilę A może Bogdan coś Ci podrzuci Pozdrawiam Lucyno i Bogdanie

think: ehh dobra Jaguś, ja znikam jestem padnięta, ale liczę że jak tu zajrzę inszym razem to znajdę jakieś zadanko dla mnie nie wymagam aby było szalenie trudne, może być proste takie jak to dla Kejt

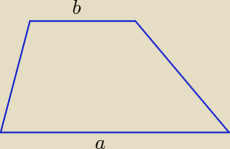
Bogdan: No to ja wrzucę zadanko. Wiemy, że w trapezie o podstawach długości a, b, odcinek łączący środki ramion ma długość

	a + b
równą średniej arytmetycznej liczb a, b, czyli		, a odcinek równoległy do podstaw,
	2

łączący ramiona i przechodzący prze punkt przecięcia przekątnych trapezu ma długość

	2ab
równą średniej harmonicznej liczb a, b, czyli		.
	a + b

Gdzie jest położony w trapezie odcinek równoległy do podstaw, łączący jego ramiona i którego długość jest równa średniej geometrycznej liczb a, b, czyli √ab. Jaką własność w trapezie ma ten odcinek?

Jaga: Dorzucam jeszcze do kompletu Gdzie jest położony w trapezie odcinek równoległy do podstaw, łączący jego ramiona i którego długość jest równa średniej kwadratowej liczb a i b. Jaką własność w trapezie ma ten odcinek?

Kejt: 1. dla każdej pary wynik będzie −1 więc wystarczy policzyć liczbę par: a_n=a₁+(n−1)r

	−a1+r+an
n=
	r

liczba par będzie taka sama jak ilość liczb dodatnich: a₁=2 r=4 a_n=2010

	−2+4+2010		2012
n=		=		=503
	4		4

503*(−1)=−503 więc: 2−3+6−7+10 −11+ ........... + 2010 −2011=−503

Kejt: Think, jak chcesz to się częstuj

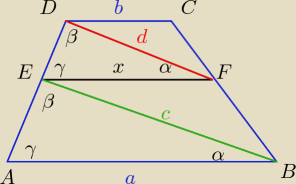
Godzio: Tak mi się wydaję że chyba dobrze Z podobieństwa: DCF ~ EFB :

b		d
	=
x		c

DEF~ABE

d		x
	=
c		a

b		x
	=
x		a

ab = x² x = √ab Ten odcinek leży między punktami przecięcia się 2 równoległych do siebie wychodzących z wierzchołków obu podstaw z ramionami trapezu ale nie wiem jaka to może być własność

Bogdan: Polecam lekturę tej strony: http://www.mimuw.edu.pl/delta/artykuly/delta1005/jaszunska.pdf Warto znać te własności trapezu.

Godzio: A to moje rozwiązanie jest w ogóle prawidłowe ?

think: tak Godzio, dla √ab odcinek łączący ramiona dzieli trapez na dwa trapezy podobne dla tego co podała Eta mamy podział na dwa trapezy o równych polach.