Procenty Marcelina: w klasie ze sprawdzianu z matematyki 9 osób czyli 36% dostało 1 ile liczy ta klasa? prosze o jakis wzór do tego

Godzio: 36% * ( ilość osób w klasie) = 9 36%x = 9 x = ?

justa1234: 36%x = 9 x = ? 36%=36/100 36/100x=9 x=9*100/36 x=900/36 x=25 Odp. Klasa liczy 25 osób.

Maciek: 36%−9 100%−x x=25

Jaga: n −− ilość osób 0,36*n= 9

	9
n=		= 25
	0,36

Gustlik: Najlepiej proporcją, tak jak zrobił Maciek: 36 % − 9 100 % − x

	9*100
x=		=25
	36

Jaga: Te Wasze proporcje to mnie wkurzają kalkulator do ręki i masz:

	9
0,36n=9 => n=		=......... dzielenie na kalkulatorze i wynik gotowy n= 25
	0,36

Bogdan: Mnie też proporcje wkurzają, dopuszczam je w zadaniach z figurami podobnymi. W pozostałych zagadnieniach, np. w zadaniach z procentami, cenami, są przejawem nieumiejętności praktycznego zastosowania matematycznego myślenia.

	9		1
Np. w tym zadanku od razu widać, że 1% to		=		, a 100% to liczba 100 razy
	36		4

	1
większa od		, czyli 25. Oczywiście w tle tego rozumowania występuje proporcja, ale
	4

bardziej elegancki i dojrzały zapis rozwiązania nie zawiera proporcji: 9 : 36 * 100 = 25 Jak widać, jest to zadanie arytmetyczne, nie ma potrzeby wprowadzać oznaczeń literowych. Jeśli nie możemy obejść się bez wprowadzenia literek, to można zapisać równanie: 36%x = 9 (jak u Godzia) lub równoważne równanie: 0,36n = 9 (jak u Ety czyli Jagi).

Jaga:

Gustlik: Tak, tylko wielu osobom myli się, kiedy mamy mnożyć przez 100 %, a kiedy dzielić. Proporcja eliminuje ten problem. Dla mnie też jest lepiej zamienić % na ułamek i kalkulatorem policzyć, ale niektórym uczniom się myli.

Jaga: A jak jesteśmy na zakupach i dostajemy 15% rabatu to też układamy proporcję z "x" ?

Gustlik: Jaga − trzeba znać różne sposoby, ja bym zrobił 0,85*x, ale nie każdy tak zrobi. Dlatego tym, co nie kumają proponuję proporcje.

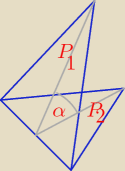
Godzio: Jeśli mogę się wtrącić to lepiej pokazać łatwiejszą i szybszą metodę ale podać przykład bo wtedy lepiej się kojarzy. Tak jak Eta teraz napisała 15% rabatu to że tak powiem każdy głupi będzie wiedział że x − 15%x = 85%x bo to do czegoś mu się przyda i tam gdzie się da trzeba pokazywać obrazowe przykłady Np. Nie wiem czemu nie mogłem skumać twierdzenia (rysunek) P₂ = P₁ * cosα Nauczyciel podał przykład że wykorzystuje się to np. przy dachach czy coś w tym rodzaju i teraz z tym to kojarzę i zapamiętuję może to nie jest za ciekawy przykład ale zawsze Zawsze gdzieś można znaleźć sposób żeby pokazać obrazowo