trygonometria
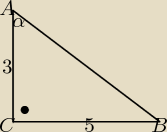
Merka: Dany jest trójkąt ABC o kącie prostym przy wierzchołku C i bokach BC=5 AC=3 AB=
√34 Jeśli kąt
CAB ma miarę α to wartośc wyrażenia sinα+cosα jest równa
mi wychodzi: sinα+cosα= 8 przez
√34
i co dalej trzeba zrobic

pomoże ktoś?
12 sie 09:55
Maciek: Jeśli dobrze jest policzone no to dalej usuwamy niewymierność z mianownika
| | 8 | | √34 | | 8√34 | | 2√34 | |
|
| * |
| = |
| = |
| |
| | √34 | | √34 | | 34 | | 17 | |
Następnie z jedynki trygonometrycznej.
sin
2α+cos
2α=1
12 sie 10:18
Radosław 2: Absolutnie nic,udało ci się rozwiązać zadanie.Ewentualnie można by jeszcze wyrugować
pierwiastek z mianownika i będziesz już całkiem do przodu
12 sie 10:24
Maciek:
| | 8 | |
sinα+cosα= |
| i dalej niewymierność  |
| | √34 | |
12 sie 10:27
Maciek: Jak się Radosławie robi podczas rysowania pierwiastek nad bokiem trójkąta

?
12 sie 10:29
Merka: nom spoko dziękuje

12 sie 14:28
Merka: a wynik to chyba 4√34przez 17
12 sie 14:36
Eta:
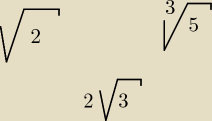 Maciek
Maciek
rysujesz symbol pierwiastka , tak jak rysujesz figury ( linią ciągłą)

12 sie 14:43
Eta:
ok

bo:
| | 8 | | 8*√34 | | 8*√34 | | 4√34 | |
sinα+ cosα= |
| = |
| = |
| = |
| |
| | √34 | | √34*√34 | | 34 | | 17 | |
12 sie 14:48
 pomoże ktoś?
pomoże ktoś?


 ?
?

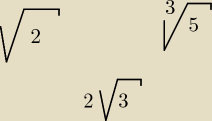 Maciek
rysujesz symbol pierwiastka , tak jak rysujesz figury ( linią ciągłą)
Maciek
rysujesz symbol pierwiastka , tak jak rysujesz figury ( linią ciągłą)

 bo:
bo: