Uzasadnij, że... nierówności trójkąta.
Matbaza: Punkt X jest dowolnym punktem leżacym wewnątrz równoległoboku ABCD.
Wykorzystując nierówności trójkąta uzasadnij, że |AX| < |BX|+|CX|+|DX|.
11 sie 13:47
bzzz:
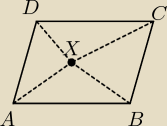
Nierówności trójkąta:
|AX| < |XB| + |AB|
|AX| < |XD| + |AD|
−−−−−−−−−−−−−−−−−−−−−−−−− +
2|AX| < |XB| +
|AB| + |XD| +
|AD|
korzystamy z tego, że w równoległoboku
|AB| = |DC| i
|AD| = |BC|
|BC| < |XC| + |XB|
|CD| < |XD| + |XC|
2|AX| < |XB| +
|XD| + |XC| + |XD| +
||XC| + |XB| = 2|XB| + 2|XD| + 2|XC| / :2
|AX| < |XB| + |XC| + |XD| ckd
11 sie 14:04
Matbaza: Serdecznie dziękuję. Czy wiesz moze z jakiej książki pochodzą te zadania? Pozdrawiam. P.
11 sie 14:10
bzzz: Niestety nie. Ogólnie nie miałam do czynienia z wieloma wydaniami stricte matematycznymi...
Jeśli Cię to bardzo nurtuje, to muisisz poczekać aż pojawi się Eta ona ma pamięć fenomenalną,
całkiem możliwe, że będzie w stanie wskazać zbiór, z którego te zadania pochodzą.
11 sie 14:31
Stanislaw: Ten zbiór to "Matematyka" Oficyna Edukacyjna Krzysztof Pazdro (Kurczab, Kurczab, Świda)
3 lut 19:31
 Nierówności trójkąta:
|AX| < |XB| + |AB|
|AX| < |XD| + |AD|
−−−−−−−−−−−−−−−−−−−−−−−−− +
2|AX| < |XB| + |AB| + |XD| + |AD|
korzystamy z tego, że w równoległoboku |AB| = |DC| i |AD| = |BC|
|BC| < |XC| + |XB|
|CD| < |XD| + |XC|
2|AX| < |XB| + |XD| + |XC| + |XD| + ||XC| + |XB| = 2|XB| + 2|XD| + 2|XC| / :2
|AX| < |XB| + |XC| + |XD| ckd
Nierówności trójkąta:
|AX| < |XB| + |AB|
|AX| < |XD| + |AD|
−−−−−−−−−−−−−−−−−−−−−−−−− +
2|AX| < |XB| + |AB| + |XD| + |AD|
korzystamy z tego, że w równoległoboku |AB| = |DC| i |AD| = |BC|
|BC| < |XC| + |XB|
|CD| < |XD| + |XC|
2|AX| < |XB| + |XD| + |XC| + |XD| + ||XC| + |XB| = 2|XB| + 2|XD| + 2|XC| / :2
|AX| < |XB| + |XC| + |XD| ckd