 1/ wykaż,że dla liczb rzeczywistych nieujemnych a,b,c zachodzi nierówność:
1/ wykaż,że dla liczb rzeczywistych nieujemnych a,b,c zachodzi nierówność:
| a+b+c | a | b | c | |||||
≤ | + | + | ||||||
| 1+a2+b2+c2 | 1+a2 | 1+b2 | 1+c2 |
 znaczy dzisiaj ale jak wstanę ,Dobranoc
znaczy dzisiaj ale jak wstanę ,Dobranoc
 ...... Miłych snów Dobranoc
...... Miłych snów Dobranoc 
 ta nierówność kojarzy mi się tylko z jednym
ta nierówność kojarzy mi się tylko z jednym







 i cierpliwie czekam
i cierpliwie czekam
 Dobranoc, miłych snów
Dobranoc, miłych snów 
 a ja co mam robić?
a ja co mam robić? 

 ja chcę, ja potrafię to zadanko
ja chcę, ja potrafię to zadanko 
 ?
?

 , przepraszam, że wchodzę w zadania nie adresowane do wszystkich,
ale widzę, że zadania 1 nie udało się dotąd ruszyć, więc zdecydowałem się postawić
pierwszy krok.
Zauważamy, że przy podanym założeniu: a ≥ 0, b ≥ 0, c ≥ 0
wyrażenia w mianownikach są dodatnie, w licznikach są nieujemne oraz że:
, przepraszam, że wchodzę w zadania nie adresowane do wszystkich,
ale widzę, że zadania 1 nie udało się dotąd ruszyć, więc zdecydowałem się postawić
pierwszy krok.
Zauważamy, że przy podanym założeniu: a ≥ 0, b ≥ 0, c ≥ 0
wyrażenia w mianownikach są dodatnie, w licznikach są nieujemne oraz że:
| a | a | ||
< | |||
| 1 + a2 + b2 + c2 | 1 + a2 |
| b | b | ||
< | |||
| 1 + a2 + b2 + c2 | 1 + b2 |
| c | c | ||
< | |||
| 1 + a2 + b2 + c2 | 1 + c2 |


 a Ty im
właściwie podałeś już gotowca
a Ty im
właściwie podałeś już gotowca 

| 1 + a2 + b2 + c2 − 1 − a2 | ||
0 ≤ a * | + b * .... + c * .... | |
| (1+a2+b2+c2)(1+a2) |
| b2 + c2 | ||
0 a * | + b * .... + c * .... | |
| (1+a2+b2+c2)(1+a2) |
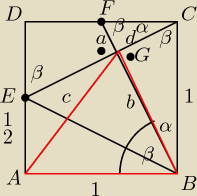 α + β = 90
α + β = 90
| √5 | √5 | |||
a + b = | => b = | − a | ||
| 2 | 2 |
| 1 | ||
a2 + d2 = | ||
| 4 |
| 1 | ||
d2 = | − a2 | |
| 4 |
| d | b | ||
= | |||
| a | d |
| √5a | ||
0,25 − a2 = | − a2 | |
| 2 |
| √5 | ||
a = | ||
| 10 |
| √5 | √5 | |||
b = | − | |||
| 2 | 10 |
| 5√6 − √5 | 4√5 | 2√5 | ||||
b = | = | = | ||||
| 10 | 10 | 5 |
| 2√5 | ||
b = | ||
| 5 |
| 1 | √5 | |||
cosβ = U{a}{ | = 2a = | |||
| 2 | 5 |
| 20 | 2√5 | √5 | ||||
c2 = | + 1 − 2 * | * | ||||
| 5 | 5 | 5 |
| 4 * 5 | ||
c2 = 5 − | ||
| 5 |
| 4 | 4 | |||
c2 = | + 1 − | |||
| 5 | 5 |

| x1 + x2 | ||
xw = | ||
| 2 |
 Zadanie 1. Drugi krok polega na dodaniu stronami nierówności zapisane w kroku pierwszym
i natychmiast otrzymujemy rozwiązanie.
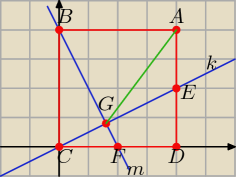
Zadanie 2. Zachęcam do rozwiązywania zadań z figurami geometrycznymi metodami
geometrii analitycznej, niekiedy ta droga jest prostsza. Tak można postąpić w zadaniu 2.
Nakładamy "sprytnie" na rysunek kwadratu układ współrzędnych i oznaczamy:
Zadanie 1. Drugi krok polega na dodaniu stronami nierówności zapisane w kroku pierwszym
i natychmiast otrzymujemy rozwiązanie.
Zadanie 2. Zachęcam do rozwiązywania zadań z figurami geometrycznymi metodami
geometrii analitycznej, niekiedy ta droga jest prostsza. Tak można postąpić w zadaniu 2.
Nakładamy "sprytnie" na rysunek kwadratu układ współrzędnych i oznaczamy:
| 1 | 1 | |||
A(1, 1), B(0, 1), C(0, 0), D(1, 0), E(1, | ), F( | , 0). | ||
| 2 | 2 |
| 1 | ||
k: y = | x, m: y = −2x + 1 | |
| 2 |
| 2 | 1 | |||
Otrzymujemy: G = ( | , | ). | ||
| 5 | 5 |
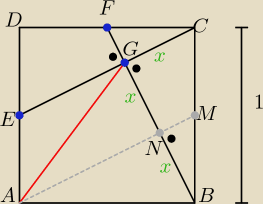 podaję taki dowód:
ΔCGF ~ Δ BCF w skali 1:2 ( uzasadnić)
to: ICGI= x i IBGI= 2x dla x>0
Prowadzimy prostą AM II do prostej EC
otrzymująac punkty N i M
ΔMNM przystaje do ΔCGM ( uzasadnić )
to IBNI = ICGI = INGI= x i prosta AM jest symetralną odcinka BG
zatem ΔABG jest równoramienny o ramieniu długości IABI= IAGI =1
c.n.u
podaję taki dowód:
ΔCGF ~ Δ BCF w skali 1:2 ( uzasadnić)
to: ICGI= x i IBGI= 2x dla x>0
Prowadzimy prostą AM II do prostej EC
otrzymująac punkty N i M
ΔMNM przystaje do ΔCGM ( uzasadnić )
to IBNI = ICGI = INGI= x i prosta AM jest symetralną odcinka BG
zatem ΔABG jest równoramienny o ramieniu długości IABI= IAGI =1
c.n.u
 Twierdzenie jest prawdziwe dla każdego kwadratu o boku długości "a"
to: IAGI= a dla a >0
Twierdzenie jest prawdziwe dla każdego kwadratu o boku długości "a"
to: IAGI= a dla a >0
 . Twoje pierwsze zadanie bardzo mi się podoba
. Twoje pierwsze zadanie bardzo mi się podoba  . Widzę, że
sama zadajesz zadania wymagające trochę pomyślunku, bo te, które na forum się pojawiały
w ostatnich tygodniach w większości przypadków sprawiały wrażenie, jakby były przeznaczone
dla poprawkowiczów i dlatego nie udzielałem się tu ostatnio, zresztą nie było mnie jakiś czas
w domu.
Pozdrawiam
. Widzę, że
sama zadajesz zadania wymagające trochę pomyślunku, bo te, które na forum się pojawiały
w ostatnich tygodniach w większości przypadków sprawiały wrażenie, jakby były przeznaczone
dla poprawkowiczów i dlatego nie udzielałem się tu ostatnio, zresztą nie było mnie jakiś czas
w domu.
Pozdrawiam 
 Staram się jak mogę podnosić poprzeczkę, bo rzeczywiście przez dłuższy czas na forum
zadania , które się pojawiały były na poziomie szk. podstawowej.
Mam wątpliwości czy poprawkowicze zdołają poprawić tę maturę, skoro mają takie
elementarne braki,że
Staram się jak mogę podnosić poprzeczkę, bo rzeczywiście przez dłuższy czas na forum
zadania , które się pojawiały były na poziomie szk. podstawowej.
Mam wątpliwości czy poprawkowicze zdołają poprawić tę maturę, skoro mają takie
elementarne braki,że  Pozdrawiam, życzę miłego wypoczynku
Pozdrawiam, życzę miłego wypoczynku 
