Stereometria 1: 1.z wycinkia koła o promieniu 6 i kącie srodkowym 225* utworzono powieszchnie boczna stożnka.oblicz objetosc stozka. 2.oblicz pole powieszchni calkowitej i objetosc ostrosupa prawidlowego trojkatnego w ktorym krawedz podstawy ma dlugosc 4 cm i tworzy z krawedzia boczna kat o mierze alfa=Pi przez 3. 3.W kulę o promienia R=10 wpisano stozek ktorego kat rozwarcia ma miare 2alfa, oblicz objętosc i pole powieszchni całkowitej 4. w stozek ktorego kat rozwarcia ma miare 2 alfa wpisano kule o promieniu R=2.oblicz objetosc i pole powiezchni całkowitej

1: 1.z wycinkia koła o promieniu 6 i kącie srodkowym 225* utworzono powieszchnie boczna stożnka.oblicz objetosc stozka. 2.oblicz pole powieszchni calkowitej i objetosc ostrosupa prawidlowego trojkatnego w ktorym krawedz podstawy ma dlugosc 4 cm i tworzy z krawedzia boczna kat o mierze alfa=Pi przez 3. 3.W kulę o promienia R=10 wpisano stozek ktorego kat rozwarcia ma miare 2alfa, oblicz objętosc i pole powieszchni całkowitej stożka 4. w stozek ktorego kat rozwarcia ma miare 2 alfa wpisano kule o promieniu R=2.oblicz objetosc i pole powiezchni całkowitej stożka

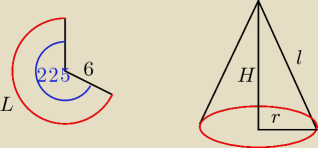
Godzio: zad. 1 R = 6 = l

	α		225
L =		* 2πR =		* 12π = 7,5π
	360		360

Długość łuku jest długością podstawy stożka: 7,5π = 2πr r = 3,75 H² + r² = l² H² = 6² − 3,75² H = ...

	1
V =		πr2 * H
	3

Dokończ.

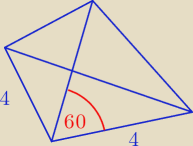
Godzio: zad 2.

	π
α =		= 60o
	3

60^o − ta informacja mówi że jest to czworościan foremny, wszystkie ściany są trójkątami równobocznymi więc nie będziemy się bawić w liczenie tylko od razu pod wzór. a = 4 P_c = a²√3

	a3√2
V =
	12

Podstaw i licz

A: dzięki

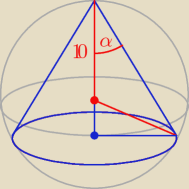
Godzio: zad. 3

	r
tgα =
	H

r = tgα * H (H − 10)² + r² = 10² H² − 20H + 100 + tg²αH² = 100 H²(1 + tg²α) − 20H = 0 H(H(1 + tg²α) − 20) = 0 −−−−−−− H = 0 odpada

	20		1
H =		−−−−−−− może znasz taki wzorek: 1 + tg2α =
	1 + tg2α		cos2α

H = 20cos²α r = 20tgα*cos²α

	r
sinα =
	l

	20tgα*cos2α		sinα		1
l =		= 20cosα −−−−−−		* cos2α *
	sinα		cosα		sinα

	1		1
V =		* πr2 * H =		π * 400tg2α * cos4α * 400cos4α =
	3		3

	160 000
=		π*sin2αcos6α
	3

P_c = πr² + πrl = 400tg²α*cos⁴α + π * 20tgα*cos²α * 20cosα = = 400sin²α*cos⁴α + π * 400sinα*cos²α*π = 400cos²αsin²α*π(sinαcos²α + 1) = = 400cos²αsin²α*π(sinα − sin³α + 1) = − 400cos²αsin²α*π(sin³α − sinα − 1) Napisz czy wynik się zgadza

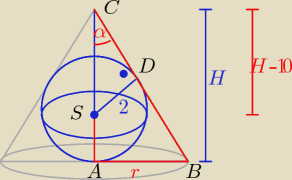
Godzio: zad. 4 Z podobieństwa: DSC ~ ABC

2		H−10
	=
r		H

	r
2H = r(H − 10) tgα =		⇒ r = tgα * H
	H

2H = tgα * H(H − 10) /: H 2 = tgαH − 10tgα

	2 + 10tgα
H =
	tgα

r = 2 + 10tgα

	r
sinα =
	l

	2 + 10tgα
l =
	sinα

	1		1		2 + 10tgα
V =		* πr2 * H =		* π(2 + 10tgα)2 *		=
	3		3		tgα

	(2 + 10tgα)3
=		*π
	3tgα

	2 + 10tgα
Pc = πr2 + πrl = π(2 + 10tgα)2 + π(2 + 10tgα) *		) =
	sinα

	1
= (2 + 10tgα)2*π( 1 +		)
	sinα

A: dziękuje jeszcze raz