 Nierówności trygonometryczne dla TOmka
Przykład pierwszy:
sin2x < sinx w przedziale <−π,π> − ja to zawsze sobie rozpisuję tak jak równanie później
wykres, czasami już nie zależy czy widać czy nie
No więc;
sin2x < sinx − rozpisujemy to tak jak zwykle:
2x = x + 2kπ v 2x = π − x + 2kπ
x = 2kπ v 3x = π + 2kπ
Nierówności trygonometryczne dla TOmka
Przykład pierwszy:
sin2x < sinx w przedziale <−π,π> − ja to zawsze sobie rozpisuję tak jak równanie później
wykres, czasami już nie zależy czy widać czy nie
No więc;
sin2x < sinx − rozpisujemy to tak jak zwykle:
2x = x + 2kπ v 2x = π − x + 2kπ
x = 2kπ v 3x = π + 2kπ
| π | 2 | |||
v x = | + | kπ − to co wyznaczyłem to są ich miejsca | ||
| 3 | 3 |
| π | ||
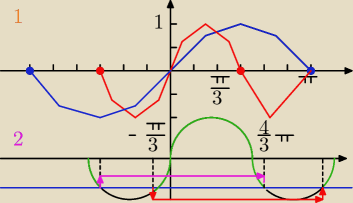
Teraz wykres 1− skale przyjmuje co | ||
| 6 |
| π | π | |||
x ∊ (− | ,0) ∪ ( | ,π> | ||
| 3 | 3 |
| √3 | ||
Przykład 2. Taki najzwyklejszy na świecie: sinx > − | ||
| 2 |
| √3 | ||
sinx > − | ||
| 2 |
| π | 4 | |||
x = − | + 2kπ v x = | π + 2kπ | ||
| 3 | 3 |
| √3 | ||
rysuję prostą linię przechodzącą przez − | lub inaczej => rysuje wykres f(x) = | |
| 2 |
| √3 | ||
− | ||
| 2 |
| √3 | ||
i sprawdzam gdzie wartości sinx są większe od − | ||
| 2 |
| π | 4 | |||
z obliczonych miejsc przecięcia wiem że punkty najbliżej zera to − | i | π | ||
| 3 | 3 |
| −π | 4 | |||
x ∊ ( | + 2kπ, | π + 2kπ) −−−− + 2kπ bo te przedziały się ciągle | ||
| 3 | 3 |
 czarno na białym wszystko wytlumaczone
czarno na białym wszystko wytlumaczone 
 pomyłeczka
pomyłeczka