Planimetria Kamil: Prosze o pomoc. Ile punktów wspólnych ma okrąg o średnicy 5 z prostą, jeśli środek tego okręgu jest oddalony od tej prostej o 4? A)0 B)2 C)3 D)1

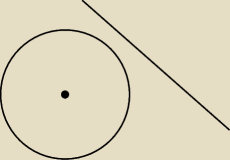
Godzio: To ile ma ?

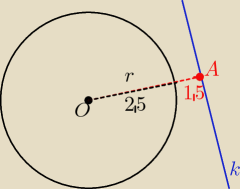
Józio: 2r=5 to r= 2,5 IOAI = 4 Odpowiedz na zadane pytanie: czy prosta k ma punkty wspólne z tym okręgiem ? i to wszystko .

Kamil: nie bardzo wiem czego jest 2r=5

Kejt: średnica to dwa promienie.. w zadaniu jest podane, że średnica ma 5. więc promień ma 2r=5

Kamil: Prosze o pomoc

Kejt: jeszcze jakiś problem?

Kamil: a srednica to od punktu O do A tak

Kejt: nie. średnica to 2r(nie ma jej zaznaczonej na rysunku). |OA| to odległość środka okręgu od prostej..

Kamil: prosze powiedz Kejt

Kejt: cóż jeszcze?

Kamil: 2 promienie to średnica dobrze mówie

Kejt: tak.

Kamil: napisane jest 2r=5 czyli dwa promienie a srednica cała ma 5 tak dobrze rozumie

Kejt: tak. Masz to napisane w treści zadania..

Kamil: ma 0 punktów z prostą tak bo musiła by prosta przylegać koło okregu tak dobrze rozumiem Kejt

Kejt: przylegać albo przecinać. Tak, ma 0 punktów wspólnych.

Kejt: jeszcze się tak z ciekawości zapytam.. która klasa?

Maciek: Kejt mi się wydaje ,że on poprawia tegoroczną maturę chociaż sam nie wiem jak można było tego nie zdać na 30%

Kejt: tak, już też zauważyłam.. Też nie wiem.. jestem w pierwszej liceum i tegoroczna matura nie sprawiła mi prawie żadnych trudności..

Maciek: No ja piszę w tym roku

Kejt: powodzenia

Maciek: Z "P" nie będzie problemu , ale chcę zdać to "R" , Dzięki

Godzio: To Macie będziemy pisać razem

Maciek: Godzio Ty jesteś w moim wieku ?

Kejt: Maciek.. nie zwracaj uwagi.. Godzio to mutant.. oczywiście nie w złym tego słowa znaczeniu..

Eta: Do tego ......z 13 XI Skorpion szczęsliwa trzynastka

Maciek: No bo mnie zaskoczył On tu 99% zadań robi w 10 sekund

Eta: "rozwali" maturę w 15 minut

Kejt: nie Ciebie jednego.. Do tej pory nie wierzę, że między nami jest tylko rok różnicy..

Maciek: Godzio może jakieś wskazówki jak dojść do takiej wprawy ? Codziennie robisz zadania czy jak ?

Kejt: pewnie śpi ze zbiorem zadań pod poduszką.. na "nocną przekąskę".

Maciek:

Godzio: Kejt thx za ten komentarz "mutant" Maciek ćwiczenia czynią mistrza − jak tu przychodziłem rok temu w październiku nie umiałem poprawnie rozwiązać równania z wartością bezwzględną Eta Podstawę na pewno ale będę ją sprawdzać kolejną 1 h bo dosłownie moje marzenie to 100% z podstawy i tak koło 96% z rozszerzenia więc nie wiem kiedy bym skończył i tak 5 razy sprawdzę, sprawdziany jak na lekcji piszę to też max 15 min i oddaje i sprawdzać mi się nie chcę i później tracę punkty np. na dodawaniu albo ostatnio zamiast x w liczniku przepisałem w mianowniku także wykorzystam to doświadczenie na maturze i będę siedzieć ile wlezie do póki nie będę pewien na 100% a na rozszerzeniu to już na pewno całe przesiedzę Sie rozpisałem jak nie chce się wam czytać to nie musicie

Kejt: hah. mam nadzieję, że nie widzisz w tym złych intencji..

Maciek: Godziu czyli dobrze zrobiłem ,że tu trafiłem ?

Godzio: Maciek powiem tyle nie robiłem żadnego zbioru zadań dopiero zacząłem w połowie 2 roku szkolnego w 2 klasie , tutaj na oko robiłem około 30 zadań dziennie czasem więcej jak był duży ruch i dzięki temu nabrałem takiej wprawy w obliczeniach że wiesz , ale to też zasługa Ety która zawsze podrzuca jakieś zadanka typu udowodnij To jest moje ulubione zadanko podane przez Etę : Udowodnij, że jeżeli długości a,b,c boków trójkąta spełniają warunek:

1		1		3
	+		=		to jeden z kątów ma miarę 60o
a+b		b+c		a+b+c

Mam nadzieję że też uda Ci się je zrobić

Eta: Tak trzymaj ......... P: 100% i R : 100% ( innej opcji nie przyjmuję

Godzio: Jasne że dobrze

Godzio: Maciek skąd jesteś ?

Maciek: Spróbuję dzisiaj ale jak wstanę bo nie mam już siłyDobranoc

Godzio: jeszcze tylko to skomentuje [P[Kejt] nie Ciebie jednego.. Do tej pory nie wierzę, że między nami jest tylko rok różnicy.. posiedź tu jeszcze rok to zobaczymy czy mnie nie prześcigniesz, ja zaczynałem w 2 klasie przygodę z forum a ty w pierwszej także wiesz tylko pamiętaj żebyś nie zaniedbała przypadkiem innych przedmiotów bo świadectwo maturalne musi jakoś przyzwoicie wyglądać

Maciek: Częstochowa

Maciek: A Ty?

Godzio: Gdybyś był z Wrocka to bym mógł Ci coś doradzić bo sporo się na politechnice dzieje ale póki co mogę Ci polecić zaglądanie co miesiąc tu: http://www.im.pwr.wroc.pl/kurs/ − jest to korespondencyjny kurs który politechnika organizuje i są bardzo ciekawe zadania, i ja właśnie w tym roku planuje wysyłać tam zadania i będą sprawdzać, jak chcesz możesz je robić i będzie można sprawdzać wyniki albo zamówić sobie ich zbiór zadań 1999 − 2004 są piekielnie trudne zadania (niektóre) ma też takie treści z pochodnych granic itd. ale większość jest na poziomie wyższym rozszerzonym także warto myślę ja właśnie kończę ten zbiór i właśnie te zadania co umieściłem są z niego ale to już jak będziesz chciał

Godzio: Ale zdaje się że kilka politechnik takie coś organizuje także warto się zorientować

Godzio: A ty Kejt skąd się wywodzisz ?

Maciek: Godzio ja narazie wolałbym ogarnąć łatwiejsze zadania z P żeby naprawiać moje braki , następnie R − bo fajnie byłoby zdać Z pewnością te zadania są fajne , ale jestem przekonany ,że są dla mnie za trudne

Maciek: Kejt już poszła Zresztą też miałem spadać, Narazie

Godzio: wrzesień 2010 −> zadanie 3 i 4 nie powinny sprawić problemu No ale dobra przerabiaj podstawę i powodzenia jak coś służę pomocą

Godzio: No narazie

Sandra: Tez bym chciala napisac mature na 100% Heh.. jeszcze daleko mi do tego.. narazie to tylko marzenia xP

Kejt: ja z Gdyni jestem. i tez się do Wrocławia na politechnikę wybieram.

Maciek: Spełnieniem moich marzeń było by 50−60% z R

Sandra: co wy robicie ze tak dobrze rozumiecie matme?

Maciek: ja nie rozumiem

Maciek: Spytaj mutanta

Sandra: heh mutancie..?

Maciek: No to wczorajszy tekst Kejt

Sandra: Do jakich szkół chodzicie Coś zwiazane z matematyka?

Maciek: Ja do LO , profil mat−geo

Kejt: a ja do liceum plastycznego..

Sandra: liceum plastyczne? chyba musisz byc wszechstronnie utalentowana

Godzio: LO profil mat − fiz − inf

Godzio: widzę że mam nowy pseudonim Sandra: co wy robicie ze tak dobrze rozumiecie matme? Odp: Robimy zadania

Kejt: "zadanie 3 i 4 nie powinny sprawić problemu" znów się wyłamuję..

Godzio: 3. To tylko wyłączenie przed nawias, a jeśli podstawisz W(cos15,sin15) to nie podstawiaj wartości tylko maksymalnie uprość 4. pierwsze wyrażenie w liczniku to wzór skróconego mnożenia (jaki ? )

	x1 + x2
wiesz że p = 1 i q = 4 => i możesz skorzystać z tego: p = xw =		jak to już masz
	2

to piszesz postać iloczynową i podstawiasz dany punkt (1,4)

Kejt: no i tu zaczynają się schody.. bo jako takiej trygonometrii nie miałam.. a tego drugiego też nie rozumiem.. tzn. obliczyłam p i próbowałam dalej podstawić, ale coś nie wychodzi..

Maciek: Godzio zastanawiałem się nad tym Twoim zadankiem co dostałeś od Ety z tym udowodnij i nie wiem Próbowałem to do wspólnego mianownika na różne sposoby i mi nie wychodzi Daj jakąś podpowiedź.

Godzio: z tego co ja uprościłem to wyszło mi tak:

	y2
W(x,y) =		− tutaj po podstawieniu sin i cos widać że x2
	(x2 + y2)(x+y)(x−y)

+ y² = 1 a tego mogłaś nie wiedzieć: cos²α − sin²α = cos2α

	sin215
czyli na końcu mamy: W(x,y) =		i to tylko uprościć
	cos30

sin15 można obliczyć tak: sin15 = sin(45 − 30} = sin45cos30 − sin30cos45 4. p = 5 wyszło CI tak ?

Godzio: Maciek Twierdzenie cosinusów

Kejt: Godziu. teoretycznie rzecz biorąc to o trygonometrii nie mam zielonego pojęcia, a o twierdzeniach tym bardziej.. w 4. samo p bez obliczania tej sumy wyszło mi 2+2√2

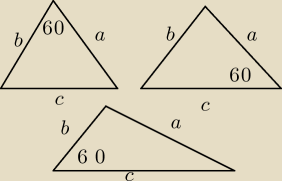
Godzio: są trzy możliwości skorzystaj z tego

Kejt: w ogóle nie wiem o co w tym chodzi.. przykro mi..

Godzio:

	...3 − ...3 − ......
p = U{ (..)(...) − (...)3}{√3 + (...)2 =		=
	√3 + .........

	20 + 15√3
		= 5
	4 + 3√3

Jeśli Ci się chce to sprawdź rachunki, a jak nie to może kiedy indziej spróbujesz

Godzio: to tw. cos i te trójkąty do tyczyły się Maćka

Godzio:

	(..)(...) − (...)3
p =		= ...
	√3 + (...)2

Kejt: już wiem dlaczego nie możemy się dogadać.. ja mówiłam o podstawie a Ty o rozszerzeniu...

Godzio: aha

Godzio: To poczekaj szybko policzę i powiem jak wyszło momencik

think: hmmm ktokolwiek widział ktokolwiek wie... nie wydaje się wam, że Basi jakoś od dłuższego czasu ni widu ni czytu?

Godzio: p = 4 mi wyszło Basia lubi czasem na dłużej nas opuścić a później wraca

think: dzięki Godzio uspokoiłeś mnie, jestem tu nie dość długo, więc to takie pierwsze dla mnie Jej zniknięcie...

Godzio: sorki poprawka p = 6

Kejt: hmm.. to może ja pokażę jak liczę.. pewnie jakiś błąd się wkradł..

	6413√8+813√64		876+843
p=		=		=
	3√64√8		856

	856(826+836)
		=826+836=2+√8=2+2√2
	856

Godzio: a może ja tak policzę żeby w 8 się nie bawić: 64^1/3 = 4 √8 = 2√2 8^1/3 = 2√2 √64 = 8 ³√64√8 = 4³√√8 = 4 * 8^1/6 = 4 * 2^1/2 = 4√2 Czyli na końcu mamy:

8√2 + 16√2		24√2
	=		= 6
4√2		4√2

zaraz poszukam błędu u Ciebie

think: mistrzu ale 8^1/3 = 2 nie 2√2

think: Także szukaj... ale u Kejt błędu nie najdziesz, bo ma dobrze

Godzio: Nie znalazłem błędu u Ciebie lecz u siebie 8^1/3 = 2

Godzio: No właśnie

robinka: tak think ma racje ma być 2

Godzio: I dlatego za podstawę się nie biorę

Maciek: Godziu ja z trygonometrii to jestem słabiutki to nawet nie mam co startować

Kejt: hmm.. to możemy się zacząć razem uczyć..

Godzio: To powiem co zrobić: piszesz twierdzenie cosinusów dla każdego możliwego kąta gdyby miał on miarę 60^o : a² = b² + c² − 2bc *cos60 a² = b² + c² − bc i analogicznie: b² = a² +c² − ac c² = a² + b² − ab jeśli przekształcisz to równanie które jest dane do jednej z tych 3 postaci to właśnie to udowodnisz Kejt Ok !

Maciek: heh tylko Ty Kejt tego nie miałaś a ja już trochę tak i niewiele to zmienia

Kejt: miałam tyle co się sama nauczyłam.. nie wiem na ile to wyjdzie.. no ale.. Godziu.. co Ty znowu knujesz?

Maciek: Kejt ja to bym zaczął od najprostszych zadań z trygonometrii jakie tylko możliwe

Kejt: zapewne realizowaliśmy różne podstawy programowe.. takie najprostsze robiłam bez większego problemu..

Godzio: Kejt o co chodzi ?

Kejt: nie wiem co to "ok!" oznaczało.

Maciek: No bo Godziu napisałeś na końcu postu do mnie : Kejt Ok !

Godzio: a nie wiem

Kejt: Patrzyłam na te, które TOmkowi napisałeś.. i dla mnie to jest czarna magia..

Godzio: Widzę że się nudzicie Może coś na rozgrzewkę ?

Maciek: no daj ale łatwe

Godzio: Te zadania co TOmkowi to dopiero jak przerobisz trygonometrie nie ma innego sposobu

Kejt: z chęcią.. tylko nie przesadzaj z poziomem. ;>

Godzio: zad 1. Wykaż że nie istnieje taka liczba rzeczywista x aby suma tej liczby i jej odwrotności była równa 1

Kejt: przerobię sama z siebie.. bo u nas w szkole matematyka ledwo raczkuje..

Maciek:

	1
Z.x+		≠1
	x

Maciek: Dz. x∊R

Godzio: x ∊ R − {0}

Maciek: sry

Kejt: to trygonometria?

Godzio: nie

Kejt: no właśnie tak dziwnie łatwo poszło..heh.

Maciek:

	1
x+		−1=0
	x

x2		1		1
	+		−		=0
x		x		x

x=0 −> sprzeczne z Dziedziną?

Godzio: kombinować dalej myślałem że to już nie sprawi problemu

Kejt: mm.. z tym zadaniem?

	1
x+		=1
	x

x²+1=x x²−x+1=0 a=1 b=−1 c=1 Δ=(−1)²−4=1−4=−3 Δ<0 => x∉R tyle wystarczy?

Maciek: tylko co by tu wykombinować ja myślałem ,że tak może być

Maciek: Tak jak Kejt jest ok

Godzio: o to chodziło Kejt

Kejt: łii

Godzio: tylko tak dziwnie napisane x ∉ R, lepiej x ∊ ∅

Maciek: Skoro mi wyszło x=0 a Dz. x∊R bez 0 to czemu nie może być ?

Godzio: To może teraz w to się pobawicie: Udowodnij, że punkt styczności okręgu wpisanego w trójkąt prostokątny z przeciwprostokątną dzieli tę przeciwprostokątną na odcinki, których iloczyn jest równy polu tego trójkąta.

Godzio: tzn tak Ty chciałeś sprowadzić to wspólnego mianownika a to Ci chyba nie wyszło

x2		1		x
	+		−		= 0
x		x		x

x2 − x + 1
	= 0 ⇔ x2 − x + 1 = 0
x

Maciek: jestem skończony

Maciek: Ja nie mam pojęcia odnośnie tego nowego..

Eta: suma liczby x i jej odwrotności jest zawsze ≠ 1 dla x ≠0

Maciek: Mam sytuację w głowie , ale nie wiem jak się do tego zabrać , ale Kejt pewnie zrobi

Kejt: cóż.. mi się udało zrobić rysunek..

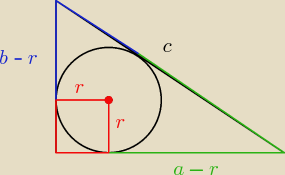
Godzio: Mamy dowieść że

	ab
(a − r)(b − r) =
	2

spróbować chociaż jak ja to robiłem to znałem wzór na promień okręgu wpisanego w trójkąt prostokątny i ten wzór możecie przy okazji sobie wyprowadzić

Maciek: Pierwsze słyszę o wzorze na promień okręgu wpisanego w trójkąt prostokątny

Godzio: Dlatego masz okazję go wyprowadzić, co prawda jest w karcie wzorów ale po co tracić czas na szukanie go ?

Maciek: Ja nie umiem go wyprowadzić

Maciek: Chyba ,że Kejt...

Godzio: c = a − r + b − r prawda/fałsz ?

Kejt: prawda?

think: udało mi się to zrobić, ale to dla mnie wy jeszcze pogłówkujcie

Maciek: prawda

think: prawda

Godzio: c = a − r + b − r c = a + b − 2r 2r = a + b − c

	a + b − c
r =
	2

No to działajcie

think: cóż... ja w zadaniu Godzia skorzystałam z oczywistego dla mnie wzoru czyli Tw. Pitagorasa

Godzio: różnie można think chcesz też coś może mam takie zadanko banalne ale jeśli się nie załapie o co chodzi może sprawić problem

think: Godzio, na chcenie to ja jestem pazerna, wszystko bym chciała tylko nie zawsze czas i możliwości pozwalają na realizację tego chcenia. Wciskałam ogóry, jestem padnięta, ale dawaj, jak coś ciekawe to się szybko ode mnie nie odczepi.

Godzio: Mając dane punkty A(−5,2) B(7,4) opisz za pomocą równania zbiór wszystkich punktów

	π
M takich że <AMB =		. Co to za zbiór ?
	2

Maciek:

	ab
ab−ar−br+r2=		/*2
	2

2ab−(a2+b−c)−(b2+a−c)+(a+b+c)2−ab
	=0
2

ab−a2−b+c−b2−a+c+a2+b2+c2+2ab+2bc+2ac
	=0
2

c2+3ab+2bc+2ac−b−a+2c
	=0
2

ja jestem w lesie

think: AB trzeba potraktować jako średnicę okręgu, wyznaczyć równanie okręgu o środku S = (1,3) i r = √148

Kejt: czyli nie tylko mi takie kolosy wychodzą..

Maciek: Kejt jak znam życie my rozwiązujemy to na"chłopski rozum" ,a taki Godziu to ma pomysł i plan jak to najszybciej zrobić

Godzio: No i o to chodziło think mówiłem że banał

Kejt: tak, też tak myślę.. ale on pewnie woli żebyśmy się z tym trochę pomęczyli..

Maciek: Ja robię jeszcze raz ale na kartce to będzie lepiej widać Godziu jeszcze nie pisz rozwiązania

Godzio: Nie spieszno mi do tego

Kejt: a ja ogłaszam kapitulację.. przynajmniej na dzisiaj.

Kejt: a nie mówiłam? On lubi się poznęcać.. ;>

think:

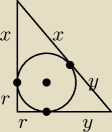
	1
mamy udowodnić, że xy = P =		(x+r)(y+r)
	2

tw.Pitagorasa (x+y)² = (x+r)² + (y+r)² 2xy = 2xr + 2yr + 2r² / :2 xy = xr + yr + r² dodam stronami xy 2xy = xy + xr + yr + r² 2xy = (x + r)((y + r) / :2

	1
xy =		(x+r)(y+r) = P ckd
	2

Maciek: Czy na końcu ma wyjść (c+a)(b−c)=0 ?

Maciek: A nie sry pomyłka

Maciek: Mam pytanko czy (a+b−c)²=a²+b²+c²+2ab−2ac−2bc ?

Godzio: tak

Maciek: Think − Twój sposób rozwiązania jest bardzo czytelny i chyba prostszy

think: dziękuję ale gdybym zrobiła tyle zadań ze wzoru na promień okręgu wpisanego w trójkąt co zadań z Pitagorasa, to pewnie zrobiłabym sposobem Godzia, niby starych drzew się nie przesadza, ale zrobienie tego metodą Godzia zostawię sobie na dzień kiedy będę miała nadmiar wolnego czasu.

Maciek: Okey poddaje się poskracałem i sprawdzałem raz i jestem przy takim czymś : c²−bc+ab−ac=0

Kejt: czyli ja mam gdzieś błąd.. w takim razie pójdę już. dobranoc

Maciek: A Ty Kejt do czego doszłaś ?

Kejt: −2a²−2b²−c²+3ac+3bc−2ab=0 więc pewnie się gdzieś walnęłam..

Maciek: Napiszę po kolei jak jechałem

think: ja też mykam spać

think: dobrej nocy pozostającym a miłych snów idącym

Maciek:

	ab
(a−r)(b−r)=		/*2
	2

ab−2ra−2rb+2r²=0

	2(a+b−c)a		2(a+b−c)b
ab−		−		+(a+b−c)2=0
	2		2

ab−(a²+ab−ca)−(ab+b²−bc)+a²+b²+c²+2ab−2ac−2bc=0 ab−a²−ab+ca−ab−b²+bc+a²+b²+c²+2ab−2ac−2bc=0 c²−bc+ab−ac=0

Godzio: Teoretycznie to się powinno od lewej do prawej dojść

Maciek: Dziękujemy Think

Maciek: Teoretycznie tak

Maciek: A jak robiłem samą lewą stronę to mam na końcu tak :

	a2+b2+2c2+4ab−3bc−3ac
L=
	2

Godzio:

Maciek: Godzio jak Ci się kiedyś będzie chciało to policz mi się już nie chce Dobranoc

Eta:

Godzio: Za moment poleczę ale już widzę że błąd zrobiłeś

Maciek: No nie wątpie bo tak by mi wyszło , ale Eta dała podobne zadanie to i tak jeszcze przy tym posiedzę,aby doprowadzić z L do P

Godzio: Jeśli robiłeś tą drogą:

	ab
(a − r)(b − r) =		to tak:
	2

	a + b − c		a + b − c		a − b + c		b − a + c
(a − r)(b − r) = (a −		)(b −		) =		*		=
	2		2		2		2

ab − a2 − bc − b2 + ab − bc + cb − ac + c2		−a2 + 2ab − b2 + c2
	=		=
4		4

2ab		c2 − a2 − b2		ab
	+		=
4		4		2

c² − a² − b² − z czym to się kojarzy ?

Maciek: to się kojarzy z wzorem ? c² −(a−b)(a+b)

bzzz: Maciek zonk tego nie można rozpisać w sposób przez Ciebie podany, jak wyciągasz nawias to sprzed obu c² −(a² + b²) = 0 z tw Pitagorasa przecież a² + ² = c²

Kejt: hmm.. czyli to koniec? tyle wystarczy?