 1. Z kuli o promieniu R wycięto ósmą część trzema wzajemnie prostopadłymi płaszczyznami przez
środek kuli. W tak otrzymaną bryłę wpisano inną kulę. Obliczyć stosunek pola powierzchni tej
kuli do pola powierzchni bryły.
2. Podstawą czworościanu ABCD jest trójkąt równoboczny ABC o boku a, ściana boczna BCD jest
trójkątem równoramiennym prostopadłym do płaszczyzny podstawy, a kąt płaski ściany bocznej
przy wierzchołku A jest równy α. Obliczyć pole powierzchni kuli opisanej na tym czworościanie
3. W ostrosłupie prawidłowym czworokątnym krawędź boczna jest nachylona do płaszczyzny podstawy
pod kątem α, a krawędź podstawy ma długość a. Obliczyć promień kuli stycznej do wszystkich
krawędzi tego ostrosłupa. Sporządzić odpowiednie rysunki.
4. Naczynie w kształcie półkuli o promieniu R ma trzy nóżki w kształcie kulek o promieniu r, 4r
< R
przymocowanych do naczynia w ten sposób, że ich środki tworzą trójkąt równoboczny, a naczynie
postawione na płaskiej powierzchni dotyka ją w jednym punkcie. Obliczyć wzajemną odległość
punktów przymocowania kulek. Sporządzić odpowiednie rysunki.
1. Z kuli o promieniu R wycięto ósmą część trzema wzajemnie prostopadłymi płaszczyznami przez
środek kuli. W tak otrzymaną bryłę wpisano inną kulę. Obliczyć stosunek pola powierzchni tej
kuli do pola powierzchni bryły.
2. Podstawą czworościanu ABCD jest trójkąt równoboczny ABC o boku a, ściana boczna BCD jest
trójkątem równoramiennym prostopadłym do płaszczyzny podstawy, a kąt płaski ściany bocznej
przy wierzchołku A jest równy α. Obliczyć pole powierzchni kuli opisanej na tym czworościanie
3. W ostrosłupie prawidłowym czworokątnym krawędź boczna jest nachylona do płaszczyzny podstawy
pod kątem α, a krawędź podstawy ma długość a. Obliczyć promień kuli stycznej do wszystkich
krawędzi tego ostrosłupa. Sporządzić odpowiednie rysunki.
4. Naczynie w kształcie półkuli o promieniu R ma trzy nóżki w kształcie kulek o promieniu r, 4r
< R
przymocowanych do naczynia w ten sposób, że ich środki tworzą trójkąt równoboczny, a naczynie
postawione na płaskiej powierzchni dotyka ją w jednym punkcie. Obliczyć wzajemną odległość
punktów przymocowania kulek. Sporządzić odpowiednie rysunki.




| π | 27 − 32cos2α | π | π | |||||
2. S = | a2 * | α ∊ ( | , | ) | ||||
| 16 | cos2α(3 − 4cos2α) | 6 | 2 |
| 9πa2 | ||
pole mi wyszło P = | ||
| cos2α |



 , a może sposób "na Kamila" − milion
postów na minute
, a może sposób "na Kamila" − milion
postów na minute  ?
?







 jesteś nieziemska
jesteś nieziemska





 RATUNKU
RATUNKU 













 !
! 
 Dzień dobry.
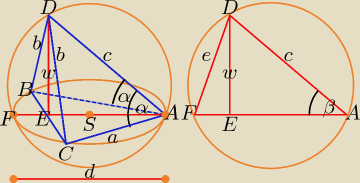
Zadanie 2.
Dzień dobry.
Zadanie 2.
| 1 | 1 | |||
|AB| = |AC| =|BC| = a, |BE| = |EC| = | a, |AE| = | a√3, |∡CAD| = |∡BAD| = α | ||
| 2 | 2 |
| 1 | 1 | 2 | ||||
|AS| = |FS| = | a√3, |ES| = |EF| = | a√3 |AF| = d = | a√3 | |||
| 3 | 6 | 3 |
| 2 | ||
|AD| = c, |AF| = d = | a√3, |DF| = e, |DE| = w, |∡EAD| = β | |
| 3 |
| 3 | ||
1) w2 + |AE|2 = c2 ⇒ w2 = c2 − | a2 | |
| 4 |
| 3 | 1 | 1 | ||||
2) w2 + |EC|2 = b2 ⇒ c2 − | a2 + | a2 = b2 ⇒ b2 = c2 − | a2 | |||
| 4 | 4 | 2 |
| 1 | 3a | |||
⇒ c2 − | a2 = a2 + c2 − 2accosα ⇒ c = | i w2 = .... | ||
| 2 | 4cosα |
| 1 | ||
e2 = w2 + |EF|2 ⇒ e2 = w2 + | a2 | |
| 12 |
| w | ||
sinβ = | , | |
| c |
| e | ce | c2e2 | ||||
2R = | = | ⇒ 4R2 = | ||||
| sinβ | w | w2 |
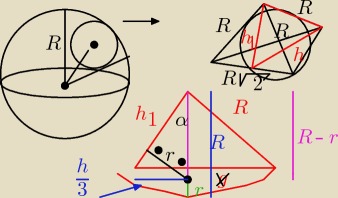 Z góry przepraszam za zagmatwane rysunki
Z góry przepraszam za zagmatwane rysunki 
| R√2 * √3 | R√6 | |||
h = | = | |||
| 2 | 2 |
| 1 | R√6 | ||
h = | |||
| 3 | 6 |
| 2 | R√6 | ||
h = | |||
| 3 | 3 |
| R2 | h1* R√2 | ||
= | |||
| 2 | 2 |
| √2R | ||
h1 = | ||
| 2 |
| 2 | ||
H2 + ( | h)2 = R2 | |
| 3 |
| R√3 | ||
H = | ||
| 3 |
| r |
| |||||||||
sinα = | = | |||||||||
| R − r | h1 |
| r |
| ||||||||
= | |||||||||
| R − r |
|
| r | R√6 | 2 | |||
= | * | ||||
| R − r | 6 | √2R |
| r | √3 | ||
= | |||
| R − r | 3 |
| √3R | R(3√3 − 3) | √3 − 1 | ||||
r = | = | = | *R | |||
| 3 + √3 | 6 | 2 |
| √3 − 1 | ||
r = | *R | |
| 2 |
| 4 − 2√3 | ||
PK = 4πr2 = 4π*R2 * | = πR2(4 − 2√3) | |
| 4 |
| 1 | 1 | 2 | 3 | 5 | ||||||
PB = | * 4π*R2 + 3 * | * πR2 = | πR2 + | πR2 = | πR2 | |||||
| 8 | 4 | 4 | 4 | 4 |
| PK | πR2(4 − 2√3) | 8 | |||||||||
= | = | (2 − √3) | |||||||||
| PB |
| 5 |

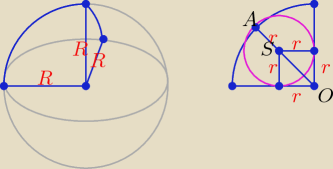 Zadanie 1.
Kula o promieniu długości R została rozcięta na 8 jednakowych brył. W jedną z tych brył
wpisano kulę o promieniu r.
|OA| = R = r√2 + r ⇒ R = r(√2 + 1) ⇒ R2 = r2(3 + 2√2)
PK = 4πr2,
Zadanie 1.
Kula o promieniu długości R została rozcięta na 8 jednakowych brył. W jedną z tych brył
wpisano kulę o promieniu r.
|OA| = R = r√2 + r ⇒ R = r(√2 + 1) ⇒ R2 = r2(3 + 2√2)
PK = 4πr2,
| 1 | 1 | 5 | 5 | |||||
PB = | *4πR2 + 3* | πR2 = | πR2 = | πr2(3 + 2√2) | ||||
| 8 | 4 | 4 | 4 |
| PK | 4πr2 | 16 | 16(3 − 2√2) | |||||||||||||
= | = | = | ||||||||||||||
| PB |
| 5(3 + 2√2) | 5 |
| 8 | |
(2− √3) | |
| 5 |
| R(√3 − 1) | ||
R = r√3 + r => R = r(√3 +1) => r = | ||
| 2 |

 a o rysunku już nie wspominając
a o rysunku już nie wspominając
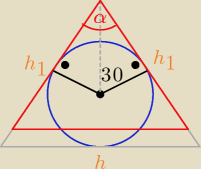
| √6 | ||
h = | R | |
| 2 |
| √2 | ||
h1 = | R | |
| 2 |
| 6 | |
R2 = R2(1 − cosα) | |
| 4 |
| 3 | |
= 1 − cosα / −1 | |
| 2 |
| 1 | |
= −cosα | |
| 2 |
| 1 | ||
cosα = − | => α = 120o | |
| 2 |
| 1 | 1 | 5 | 5 | |||||
PB = | *4πR2 + 3* | πR2 = | πR2 = | π*2r2(2 + √3) ⇒ | ||||
| 8 | 4 | 4 | 4 |
| 5 | ||
⇒ PB = | πr2(2 + √3) | |
| 2 |
| PK | 4πr2 | 8 | 8(2 − √3) | ||||||||||
= | = | = | |||||||||||
| PB |
| 5(2 + √3) | 5 |


| 2 | ||
Mógłbyś mi jeszcze tylko napisać w zadaniu 2. dlaczego |AF| = | a√3 ? | |
| 3 |
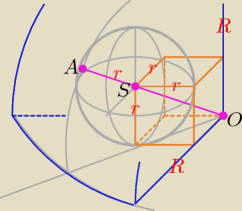 To jest szkic do zadania 1.
To jest szkic do zadania 1.
| 1 | ||
Długość promienia tego okręgu |SA| = |SB| = |SC| = | a√3 | |
| 3 |
| 2 | ||
|AF| = 2*|SA| = | a√3 | |
| 3 |
 Świetny rysunek
Świetny rysunek 
 A jeszcze co do 2 − wiadome jest że podstawia mieści się się w tym miejscu co środek tak jak
narysowałem chyba też jest taka możliwość ?
A jeszcze co do 2 − wiadome jest że podstawia mieści się się w tym miejscu co środek tak jak
narysowałem chyba też jest taka możliwość ?

 ...... ale nie za często, bo możesz dostać komen od np: omg
...... ale nie za często, bo możesz dostać komen od np: omg 
 a póki co 2 zadanka zostały
a póki co 2 zadanka zostały 