funkcja kwadratowa z parametrem aga: Bardzo proszę o pomoc! Męczę się długo i nie mogę uzyskać podanego wyniku.

	1
Dla jakiej wartości parametru k miejsca zerowe funkcji f(x) =		x2 − (k−1)x + k+3
	2

należą do zbioru A= (−2,5) ?

	1
Wynik ma być: k∊<5, 5		>. Bardzo proszę, jeśli ktoś może pomóc.
	8

Godzio: to jest poprawna treść bo jakaś dziwna ?

aga: Tak, dokładnie taka. Spróbujesz Godzio (albo ktoś inny) ? Proszę.

Godzio: Δ > 0 (k−1)² − 2(k+3) > 0 k² − 2k + 1 − 2k − 6 > 0 k² − 4k − 5 > 0 (k−5)(k+1) > 0 k ∊ (−∞,−1) ∪ (5,∞) Teraz jeśli sobie zaznaczysz na osi −2 i 5 narysujesz prowizoryczną parabolę to okaże się że musi być spełniony warunek: f(−2) > 0 i f(5) > 0 f(−2) = 2 + 2(k−1) + k + 3 > 0 2 + 2k − 2 + k + 3 > 0 3k > −3 k > − 1

	25
f(5) =		− 5(k−1) + k + 3 > 0
	2

	31
−5k + 5 + k +		> 0
	2

	41
−4k > −
	2

	41
k <
	8

	1
k < 5
	8

Odpowiedź to część wspólna

	1
k ∊ (5,5		)
	8

think: Godzio a czemu odrzuciłeś Δ = 0 przecież może być jedno podwójne rozwiązanie chyba...

aga: Dzięki Godzio. Tylko dlaczego podają wynik z przedziałem domkniętym? Może jeszcze jakieś warunki trzeba dołożyć? Ja liczyłam deltę i Δ=k² − 4k − 5. To √Δ = √k²−4k−5. I tu robiłam założenie, że k²−4k−5 ≥0, i z tego otrzymuję: k∊(−∞, −1> ∪ <5,∞). Co o tum sądzisz?

Godzio: no też prawda także dorzuć we wszystkich znakach ... lub równe

Godzio: ale moim zdaniem powinno być f(−2) > 0 i f(5) > 0 bo mają należeć do przedziału (−2,5) a nie <−2,5>

think: racja Godzio... aga tam w tym przedziale −2,5 był przedział otwarty czy zamknięty?

think: ale przy 5 jest nawias zamknięty i tak

Godzio: no tyle to tak

aga: Tak. Pozbierałam wszystko i teraz się zgadza. Dziękuję bardzo Godzio oraz think

think: eee no ja tam niewiele się przysłużyłam, Godzio to naczelny rozkminiacz tego zadania, nie jestem pewna czy wpadłabym na to, że f(−2) ≥ 0 i f(5) ≥ 0 także zadowolę się uznaniem konsultacji

think: tfu f(−2) > 0 i f(5) > 0 ostatnia myśli mi jeszcze nie wyparowała z palców

aga: W zadaniu podany był przedział otwarty (−2,5). Ale to jest przedział dla miejsc zerowych, a nie dla parametru k.

Godzio: no tak ale zobacz: podstawiamy k = 5

	1
f(x) =		x2 − 4x + 7
	2

szukamy miejsc zerowych:

1
	x2 − 4x + 7 = 0 /*2
2

x² − 8x + 14 = 0 Δ = 64 − 56 = 8 √Δ = 2√2 x₁ = 4 − 2√2 x₂ = 4 + 2√2 ≈ 6,82 czyli nie należy do przedziału (−2,5)

aga: Masz rację, Godzio, mnie też się to jednak nie zgadza. A może jest po prostu błąd w odpowiedzi?

Godzio: być może

Godzio:

	1
a nie jednak chyba dobrze jest bo popatrzyłem na		x2 a powinienem na x2 więc to na 2
	2

więc by się zgadzało

aga: Znasz zbiór arkuszy do mat. rozszerzonej z wyd. SENS ? To z tego pochodzi.

Godzio: z "SENS" się jeszcze nie spotkałem

think: no ja bym się nawet dalej posunęła w odpowiedzi na to pytanie... powiedziałabym, że z sensem to ja się spotykam coraz rzadziej natomiast bezsensu na około widzę coraz więcej

aga: Zbiór nazywa się "Matematyka z Sensem". Ale nie rozumiem, co by Ci się zgadzało na 2 ?

aga: A to dobre, think, masz rację.

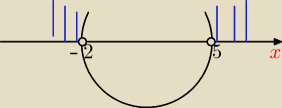
aga: A teraz chyba się przekonałam, patrząc na ten rysunek (propozycja Godzia), że f(−2) ≥0 i f(5) ≥0. Zgadzacie się?

think: aga ja jednak bardziej obstawiam, że oni się w druku pomylili, tak siłą rozpędu zamiast odpowiedzi k ∊ <5,5¹₈) dali z drugiej strony też zamknięty...

aga:

	1		1
Sprawdziłam dla k=5		i wychodzą: x1 = 5 ∉ (−2,5) i x2 = 3		∊ (−2,5). Czyli
	8		4

	1
k=5		nie może być rozwiązaniem. I tu Twoje podejrzenie błędu by się zgadzało.
	8

Tylko jak to pokazać rachunkowo, a nie sprawdzaniem?

think: widzę, że rośnie z Ciebie rasowy matematyk ale propozycja rozwiązania Godzia to już wystarczający dowód, chyba, że znajdujesz lubię w jego rozumowaniu...

think: *lukę nie lubię znaczy lubić to ja owszem lubię to i owo i tego i ową...

aga: Aha, z mojego rysunku powinno wynikać: f(−2) ≥0 ,ale f(5) >0. I wtedy otrzyma się wyliczenie : z pierwszej nierówności : k≥−1 i z drugiej: k<5¹₈.

	1
I wtedy ten błąd byłby aktualny , że powinno być <5, 5		).
	8

aga: Ale Ci nudzę, think, ale jeszcze znalazłam jedną poprawkę. Musi być też: f(−2) >0 , gdyż otrzymana liczba k=−1 nie spełnia warunku zadania. Ale odpowiedzi to nie zmienia. (bo ze znakiem ≥, rozwiązaniem byłaby jeszcze liczba −1 ! ) . To już chyba wszystko. Dzięki Ci za współpracę i pomoc.

think: wiem, przecież przyznałam rację Godziowi