Zadanie dla Maćka:)
think: Zadanie dla Maćka innych proszę o nie wpisywanie tutaj odpowiedzi 
Sprawdź, który ze zbiorów ma więcej elementów:
| | 420 − 813 | | 820 − 413 | |
A = [ |
| ; |
| ] |
| | 161/4 | | 161/4 | |
| | 820+420−813 −413 | | 820+420−813−413 | |
B=[− |
| ; |
| ] |
| | 2*161/4 | | 2*161/4 | |

8 sie 11:24
Maciek: Dziękuję , zrobię wieczorem albo jak znajdę chwilę wolnego w pracy

8 sie 11:47
think: Maciek nie poganiam

nie wiem po prostu co będę robiła w godzinach 21 −22, więc wcześniej
wpisałam zadanko niech wisi i czeka na Ciebie

przykro mi, że pracujesz w niedzielę, też mi
się zdarza na całe szczęście rzadko

8 sie 11:50
Maciek: Wyszło mi tak : A=2
21−2
14+1 , a w B jestem w takim momencie:
| | 2*223+2*222−2*216−2*215 | |
B= |
| +1  Czy jestem na dobrej drodze think? |
| | 22 | |
8 sie 15:44
think: Maciek robisz błąd,
820 = (23)20 = 23*20 zdaje się, że wszędzie masz błąd tego typu.
8 sie 15:51
Maciek: ok od nowa lecę

8 sie 16:15
think: ano trzeba będzie...

zrewidować poglądy
8 sie 16:18
Maciek: B−A=2
39 
?
8 sie 17:05
think: poczekaj policzę, ale przyznam, że pisząc te zadanie spodziewałam się wyniku 0
8 sie 17:25
think: ano tak zrobiłam błąd

dlatego nie wyszło 0
8 sie 17:28
think: zgadza się to poprawna odpowiedź

8 sie 17:29
Maciek: yupi

jak będę w domu to mam jeszcze 2 zadania z równaniem z parametrem to byś mi pomogła bo
zapomniałem jak to się liczyło

8 sie 18:10
Maciek: 1.Niech A=<2,7> oraz niech B oznacza zbiór liczb całkowitych x spełniających nierówność
Ix−mI≤2.Zbadaj liczbę elementów zbioru A∩B w zależności od parametru m.
Nie pamiętam jak się do tego zabrać czy nie czasem dla m>0 m=0 i m<0?
8 sie 21:35
Godzio:

to się normalnie rozpisuje:
|x − m| ≤ 2
x − m ≤ 2 i x − m ≥ − 2
x ≤ m + 2 i x ≥ m − 2
B = <m−2, m + 2>
szukamy A∩B
żeby była mowa o części wspólnej to musi być założenie:
m −2 ≤ 7 i m + 2 ≥ 2
m ≤ 9 i m ≥ 0
I teraz jedyny pomysł jaki przychodzi mi na myśl to podstawianie po kolei
m = 0, m = 1, m = 2 itd. i wypisywanie ilości elementów wspólnych np.
m = 0 => B = <−2,2> => 1 element wspólny ( dla 9 będzie tak samo )
m = 1 => B = <−1,3> => 2 elementy wspólne ( dla 8 tak samo)
Może poczekamy na lepszego fachowca ale myślę że ten sposób też dobry

8 sie 21:53
Maciek: m −2 ≤ 7 i m + 2 ≥ 2 , a nie może być m−2≤2 i m+2≥7? Dlaczego nie?
8 sie 21:57
Godzio: z tego byś otrzymał sprzeczność, zaraz Ci pokarze dlaczego tak a nie inaczej
8 sie 21:59
Godzio:
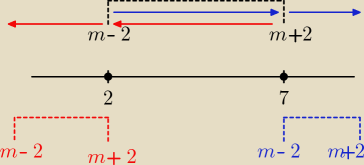
Jak widać jeśli m + 2 wyjdzie po za 2 to już nie ma mowy o części wspólnej tak samo jeśli m − 2
wyjdzie po za 7 tak samo nie ma nic wspólnego pomiędzy tymi przedziałami dlatego konieczne
jest takie a nie inne założenie
8 sie 22:02
Maciek: Ja mam w odp:
0 elementów dla m∊(−
∞,0)∪(9,+
∞)
1 element dla m∊<0,1)∪(8,9>
...
4elementy dla m∊<3,4)∪(5,6>
Jak do tego w najprostszy sposób dojść?Bo tylko to z przedziałem (−
∞,0)∪(9,+
∞) i zerem
elementów jest dla mnie logiczne

8 sie 22:17
Godzio: a no tak zawsze się zapomina tą odpowiedź
no skoro to m+ 2 wyjdzie za dwójkę albo m − 2 za 7 to jest zero elementów i to jest właśnie
przedział dla tego

8 sie 22:46
Maciek: To rozumiem

ale dlaczego jest np. 1 element wspólny dla m∊<0,1)∪(8,9> , rozumiem ,że tu jest
tylko 9 elementem wspólnym?
8 sie 22:58
Józio:
Godzio podał zakres dla "m"
m€ < 0,9> i m€C
przeprowadzamy analizę ilości elementów A n B w zależności od tego "m"
:
1/dla m€( −∞, −1> U <10, ∞) mamy −−− zbiór pusty ( 0 elementów dla An B)
bo: dla m= −1 B= < −3, 1> i A= <2, 7> to AnB= zb. pusty ( brak elementów)
dla m= 10 B= <8, 12> podobnie
dla m= 0 v m= 9 mamy jeden element wspólny
bo dla m=0 B= < −2, 2> i A= <2,7> to AnB = {2} −− 1 element
m= 9 B= < 7, 11> podobnie
dokończ dla m= 1 v m= 8 ........ otrzymasz: ( 2 elementy)
dla m= 3 v m=6 ............ (4 elementy)
dla m= 4 v m= 5 ........... ( 5 elementów)

8 sie 22:58
Józio:
oczywiście nie zapomnij jeszcze policzyć
dla m= 2 v m= 3 v m= 7 ........ otrzymasz ( 3 elementy)

8 sie 23:08
Józio:
Poprawka dla m= 2 v m= 7 ... ( 3 elementy)
bez m=3 ( bo już to liczyliśmy)
8 sie 23:11
Maciek: Ok to już czaję

i dokończę , ale jeszcze mam coś takiego:
Ix−mI+Ix−7I=3 − wyznacz te wartości parametru m dla których równanie ma nieskończenie wiele
rozwiązań.
8 sie 23:14
think: ach musisz tak dobrać m aby suma tych dwóch wartości bezwzględnych była stała = 3

8 sie 23:33
think: zrobiłam sobie wolne popołudnie, mój dziadek za dwa dni kończyłby 100 lat gdyby żył, więc
wybraliśmy się na cmentarz, nie ma co się łudzić, że uda nam się to w tygodniu...
8 sie 23:34
Maciek: Czyli opuszczać wartości bezwględne : x−m+x−7=3 v −x+m−x+7=3 ?
8 sie 23:35
think: 1o x − m ≥ 0 i x + 7 ≤ 0
x ≥ m i x ≤ −7
wtedy opuszczamy wartości bezwzględne zmieniając odpowiednio znaki
x − m − x + 7 = 3
−m = −4
m = 4 wychodzi nam sprzeczność, bo x nie może być x ≥ 4 i zarazem x ≤ −7
2o x − m ≤ 0 i x + 7 ≥ 0
x ≤ m i x ≥ −7
−x + m + x − 7 = 3
m = 10
8 sie 23:42
think: chodzi o te przypadki kiedy iksy nam się uproszczą.
8 sie 23:43
think: chociaż przyznaję dziwne jest to zadanie... masz odpowiedzi?
8 sie 23:45
Maciek: Dlaczego zawsze zapisujesz x+7 skoro w wartości jest x−7 , a parametr przepisujesz z minusem?
I jak dobrać założenia

?
8 sie 23:46
Maciek: Odp. m=4 v m=10
8 sie 23:47
think: błąd ludzki, wzrok widać nie ten.... ma być oczywiście x − 7 popraw w takim razie i zobaczmy
jak Tobie wyjdzie.
8 sie 23:51
Godzio:
Najlepiej rozpisz sobie to na wszystkie możliwe przypadki
|x − m| + |x − 7| = 3
x ≥ m x ≥ 7
x − m + x − 7 = 3 => 2x − m = 10
v
x ≥ m x < 7
x − m − x + 7 = 3 => m = 4
v
x < m x ≥ 7
− x + m + x − 7 = 3 => m = 10
v
x < m x < 7
− x + m − x + 7 = 3 => −2x + m = − 4 => 2x − m = 4
I wydaje mi się że tam gdzie jest 2x − m = 4 i 2x − m = 10 nawzajem się wykluczają więc
jedynymi rozwiązaniami jest m = 4 v m = 10 ale głowy nie dam
8 sie 23:52
Maciek: Taka jest odpowiedź Godzio

,rzeczywiście rozpisanie na wszystkie przypadki ułatwia sprawę

8 sie 23:56
Józio:

8 sie 23:58
think:
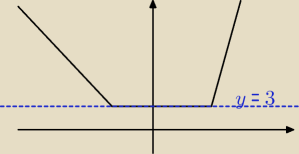
masz przykładowy rysunek sumy dwóch wartości bezwzględnych. Ponieważ chcemy aby równanie miało
nieskończenie wiele rozwiązań, to znaczy, że nasz wykres nie może przecinać w pewnych punktach
prostej y=3 ale na pewnym odcinku musi się na nią nakładać, tak jak Ci to narysowałam na
rysunku.
Jak się opuszcza wartości bezwzględne rozpatrujemy przypadki gdy ax + b > 0 to po opuszczeniu
kresek mamy samo ax + b, natomiast jeżeli jest ujemne to wystarczy zmienić −(−) da nam plus
dlatego jeśli zawartość wartości bezwzględnej jest ujemna to po jej opuszczeniu piszemy
−(zawartość między kreskami wart. bezwzgl.)
a jak z dodawania dwóch wartości bezwzględnych dostać aby iksy nam się uprościły, po prostu
jeden nawias musi być dodatni a drugi ujemny i na odwrót i ot cała fizozofia

8 sie 23:59
Maciek: Mam jeszcze coś takiego i nie wiem jak się do tego zabrać :
| | 5 | | a | | 7 | |
Liczby naturalne a i b spełniają warunek |
| < |
| < |
| .Wyznacz najmniejszą możliwą |
| | 31 | | b | | 43 | |
wartość b.
9 sie 00:00
think: no tak ja mam przebłyski a on wykonuje rzetelną pracę

9 sie 00:00
think: cóż najwygodniej to chyba sprowadzić do wspólnego mianownika?
9 sie 00:01
Maciek: i co dalej

?
9 sie 00:03
think: a sprowadziłeś?
9 sie 00:05
Godzio: | | 1 | |
a wynik to może 6 |
|  ? |
| | 6 | |
9 sie 00:05
9 sie 00:05
think: ale NWD(31,43) = 1....
9 sie 00:06
9 sie 00:06
Maciek: aa ^^ pojechałem na skróty

9 sie 00:07
think: | | 216 | |
czyli po środku musi być |
| |
| | 1333 | |
9 sie 00:07
think: a ani 31 ani 43 nie jest dzielnikiem 216
9 sie 00:08
think: czyli to jest najmniejsza możliwa liczba.
9 sie 00:09
Godzio:

myślałem że jakieś trudniejsze że coś więcej niż do wspólnego mianownika i kombinowałem

9 sie 00:09
think: choć raz Lucynka górą

9 sie 00:10
Godzio:
Maciek ? Wynik się zgadza ?
9 sie 00:11
Maciek: Odpowiedź jest b=37
9 sie 00:12
Godzio:
to rzeczywiście Lucynka górą

9 sie 00:13
Maciek: | | 1 | |
Godzio 6 i |
| to na logikę a tu zaskoczenie  |
| | 6 | |
9 sie 00:15
Maciek: To co macie jakieś pomysły

?
9 sie 00:20
think: czyli kolejne liczby pierwsze...
9 sie 00:20
think: no jeszcze 41 mogło być.. ale jest większe od 37
9 sie 00:21
Maciek: Możesz jaśniej

?
9 sie 00:22
think: 31 jest liczbą pierwszą dzieli się tylko przez 1 i przez samą siebie tak samo 43.
9 sie 00:23
Maciek: No okey ale dlaczego 37?
9 sie 00:23
think: bo też jest liczbą pierwszą, zaraz sprawdzę czy dla 41 też by wyszło
9 sie 00:25
think: Maciek, między dwie liczby można wpisać nieskończenie wiele liczb, może trzeba było iść w
kierunku 5 < a < 7 więc a = 6 to ile będzie wynosiło b. czasem potrzeba szczęścia, no chyba,
że Godzio ma lepsze wyjaśnienie

9 sie 00:27
Godzio: lepszego nie mam

9 sie 00:29
think: 41 odpada, bo a nie wychodzi naturalne.
9 sie 00:29
Maciek: Acha czyli pomiędzy 31 a 43 najmniejszą liczbą pierwszą jest 37

A nie można by tam dać np.
32 − co prawda nie jest pierwsza ale by pasowała

?
9 sie 00:30
think: możesz sprawdzić

pamiętaj, że a też musi być naturalne.
9 sie 00:31
Maciek: Nie pasuje

dobra kończę bo już mi się dziś znaczy "wczoraj" nie chce myśleć

Dziękuje
wam

P.S. Wiem ,że to portal matematyczny ,ale Godzio "pokaże" się pisze przez z z kropką

9 sie 00:37
Maciek: Józio Odp. jest b=37 jak coś

9 sie 00:38
Godzio: gdzie ja to napisałem

?
9 sie 00:42
Godzio: dobra tam

Ja też już lecę spać dobranoc

9 sie 00:44
think: ano a ja jeszcze pomyślę czemu tak, ale też mam dość... Maciek heheh dobrze, że ja na mozilli

dopiero byś zobaczył co oznacza polska jezyk trudna jezyk

9 sie 00:46
Eta:
No to tak:
| | 5+7 | |
średnia arytmetyczna liczników |
| = 6
|
| | 2 | |
| | 31+43 | |
średnia arytmetyczna mianowników |
| = 37
|
| | 2 | |
b= 37
pasuje?

9 sie 00:46
think: Eto a ma to jakieś wyjaśnienie?

czy dopasowujesz rozwiązanie do wyniku

9 sie 00:47
Józio:
Dobranoc

 Józio
Józio jest bardzo śpiący

9 sie 00:58
think: Dobrej nocy

9 sie 01:12
Eta:
Wyjaśniam:
licznik najmniejszy całkowity : 5, 6, 7
| | 5+7 | |
5,a,7 => a= |
| = 6 −−− średnia arytmetyczna
|
| | 2 | |
to i mianownik najmniejszy całkowity ( też średnia arytmetyczna)
| | 31+43 | |
31,b, 43 => b= |
| = 37
|
| | 2 | |
9 sie 01:12
think: i tak jest zawsze? kurcze nigdy się z tym nie spotkałam, ale na pewno zapamiętam

9 sie 01:13
Maciek: Również teraz zapamiętam

9 sie 23:13
bajka:
to i ja też

9 sie 23:17
b.: Nie do konca wierze w to wyjasnienie, np.
wg metody Ety:
| | 5+7 | | 23+27 | |
a = |
| = 6 b = |
| = 25 |
| | 2 | | 2 | |
| | 5 | | 6 | | 7 | |
|
| < |
| < |
| −− to sie zgadza, |
| | 23 | | 25 | | 27 | |
ale mamy tez
w oryginalnym zadaniu mozna postepowac tak
5b < 31a i 43a < 7b
35b < 217a i 215a < 35b
czyli
215a < 35b < 217a
oczywiscie im mniejsze b, tym mniejsze a, i na odwrot; sprawdzamy wiec po kolei:
a=1: 35b = 216 sprzecznosc,
a=2: 35b ∊ (430, 434) −− sprzecznosc
itd., az dojdziemy do rozwiazania
10 sie 09:22
b.: A swoja droga, metoda Ety bierze sie z nastepujacej nierownosci:
| | a | | c | | a | | a+c | | c | |
jesli |
| < |
| i a,b,c,d>0, to |
| < |
| < |
| |
| | b | | d | | b | | b+d | | d | |
moze to byc nierownosc dla Kejt

10 sie 09:27
 Sprawdź, który ze zbiorów ma więcej elementów:
Sprawdź, który ze zbiorów ma więcej elementów:


 nie wiem po prostu co będę robiła w godzinach 21 −22, więc wcześniej
wpisałam zadanko niech wisi i czeka na Ciebie
nie wiem po prostu co będę robiła w godzinach 21 −22, więc wcześniej
wpisałam zadanko niech wisi i czeka na Ciebie przykro mi, że pracujesz w niedzielę, też mi
się zdarza na całe szczęście rzadko
przykro mi, że pracujesz w niedzielę, też mi
się zdarza na całe szczęście rzadko 
 Czy jestem na dobrej drodze think?
Czy jestem na dobrej drodze think?
 zrewidować poglądy
zrewidować poglądy
 ?
?
 dlatego nie wyszło 0
dlatego nie wyszło 0

 jak będę w domu to mam jeszcze 2 zadania z równaniem z parametrem to byś mi pomogła bo
zapomniałem jak to się liczyło
jak będę w domu to mam jeszcze 2 zadania z równaniem z parametrem to byś mi pomogła bo
zapomniałem jak to się liczyło 
 to się normalnie rozpisuje:
|x − m| ≤ 2
x − m ≤ 2 i x − m ≥ − 2
x ≤ m + 2 i x ≥ m − 2
B = <m−2, m + 2>
szukamy A∩B
żeby była mowa o części wspólnej to musi być założenie:
m −2 ≤ 7 i m + 2 ≥ 2
m ≤ 9 i m ≥ 0
I teraz jedyny pomysł jaki przychodzi mi na myśl to podstawianie po kolei
m = 0, m = 1, m = 2 itd. i wypisywanie ilości elementów wspólnych np.
m = 0 => B = <−2,2> => 1 element wspólny ( dla 9 będzie tak samo )
m = 1 => B = <−1,3> => 2 elementy wspólne ( dla 8 tak samo)
Może poczekamy na lepszego fachowca ale myślę że ten sposób też dobry
to się normalnie rozpisuje:
|x − m| ≤ 2
x − m ≤ 2 i x − m ≥ − 2
x ≤ m + 2 i x ≥ m − 2
B = <m−2, m + 2>
szukamy A∩B
żeby była mowa o części wspólnej to musi być założenie:
m −2 ≤ 7 i m + 2 ≥ 2
m ≤ 9 i m ≥ 0
I teraz jedyny pomysł jaki przychodzi mi na myśl to podstawianie po kolei
m = 0, m = 1, m = 2 itd. i wypisywanie ilości elementów wspólnych np.
m = 0 => B = <−2,2> => 1 element wspólny ( dla 9 będzie tak samo )
m = 1 => B = <−1,3> => 2 elementy wspólne ( dla 8 tak samo)
Może poczekamy na lepszego fachowca ale myślę że ten sposób też dobry 
 Jak widać jeśli m + 2 wyjdzie po za 2 to już nie ma mowy o części wspólnej tak samo jeśli m − 2
wyjdzie po za 7 tak samo nie ma nic wspólnego pomiędzy tymi przedziałami dlatego konieczne
jest takie a nie inne założenie
Jak widać jeśli m + 2 wyjdzie po za 2 to już nie ma mowy o części wspólnej tak samo jeśli m − 2
wyjdzie po za 7 tak samo nie ma nic wspólnego pomiędzy tymi przedziałami dlatego konieczne
jest takie a nie inne założenie


 ale dlaczego jest np. 1 element wspólny dla m∊<0,1)∪(8,9> , rozumiem ,że tu jest
tylko 9 elementem wspólnym?
ale dlaczego jest np. 1 element wspólny dla m∊<0,1)∪(8,9> , rozumiem ,że tu jest
tylko 9 elementem wspólnym?


 i dokończę , ale jeszcze mam coś takiego:
Ix−mI+Ix−7I=3 − wyznacz te wartości parametru m dla których równanie ma nieskończenie wiele
rozwiązań.
i dokończę , ale jeszcze mam coś takiego:
Ix−mI+Ix−7I=3 − wyznacz te wartości parametru m dla których równanie ma nieskończenie wiele
rozwiązań.

 ?
?
 ,rzeczywiście rozpisanie na wszystkie przypadki ułatwia sprawę
,rzeczywiście rozpisanie na wszystkie przypadki ułatwia sprawę 

 masz przykładowy rysunek sumy dwóch wartości bezwzględnych. Ponieważ chcemy aby równanie miało
nieskończenie wiele rozwiązań, to znaczy, że nasz wykres nie może przecinać w pewnych punktach
prostej y=3 ale na pewnym odcinku musi się na nią nakładać, tak jak Ci to narysowałam na
rysunku.
Jak się opuszcza wartości bezwzględne rozpatrujemy przypadki gdy ax + b > 0 to po opuszczeniu
kresek mamy samo ax + b, natomiast jeżeli jest ujemne to wystarczy zmienić −(−) da nam plus
dlatego jeśli zawartość wartości bezwzględnej jest ujemna to po jej opuszczeniu piszemy
−(zawartość między kreskami wart. bezwzgl.)
a jak z dodawania dwóch wartości bezwzględnych dostać aby iksy nam się uprościły, po prostu
jeden nawias musi być dodatni a drugi ujemny i na odwrót i ot cała fizozofia
masz przykładowy rysunek sumy dwóch wartości bezwzględnych. Ponieważ chcemy aby równanie miało
nieskończenie wiele rozwiązań, to znaczy, że nasz wykres nie może przecinać w pewnych punktach
prostej y=3 ale na pewnym odcinku musi się na nią nakładać, tak jak Ci to narysowałam na
rysunku.
Jak się opuszcza wartości bezwzględne rozpatrujemy przypadki gdy ax + b > 0 to po opuszczeniu
kresek mamy samo ax + b, natomiast jeżeli jest ujemne to wystarczy zmienić −(−) da nam plus
dlatego jeśli zawartość wartości bezwzględnej jest ujemna to po jej opuszczeniu piszemy
−(zawartość między kreskami wart. bezwzgl.)
a jak z dodawania dwóch wartości bezwzględnych dostać aby iksy nam się uprościły, po prostu
jeden nawias musi być dodatni a drugi ujemny i na odwrót i ot cała fizozofia

 ?
?
 ?
? 
 myślałem że jakieś trudniejsze że coś więcej niż do wspólnego mianownika i kombinowałem
myślałem że jakieś trudniejsze że coś więcej niż do wspólnego mianownika i kombinowałem




 ?
?
 ?
?


 A nie można by tam dać np.
32 − co prawda nie jest pierwsza ale by pasowała
A nie można by tam dać np.
32 − co prawda nie jest pierwsza ale by pasowała  ?
?
 pamiętaj, że a też musi być naturalne.
pamiętaj, że a też musi być naturalne.
 dobra kończę bo już mi się dziś znaczy "wczoraj" nie chce myśleć
dobra kończę bo już mi się dziś znaczy "wczoraj" nie chce myśleć  Dziękuje
wam
Dziękuje
wam P.S. Wiem ,że to portal matematyczny ,ale Godzio "pokaże" się pisze przez z z kropką
P.S. Wiem ,że to portal matematyczny ,ale Godzio "pokaże" się pisze przez z z kropką 

 ?
?
 Ja też już lecę spać dobranoc
Ja też już lecę spać dobranoc 
 dopiero byś zobaczył co oznacza polska jezyk trudna jezyk
dopiero byś zobaczył co oznacza polska jezyk trudna jezyk

 czy dopasowujesz rozwiązanie do wyniku
czy dopasowujesz rozwiązanie do wyniku 

 Józio jest bardzo śpiący
Józio jest bardzo śpiący 




