Mam takie 2 zadania. Maciek: 1.Wyznacz wszystkie pary liczb naturalnych,których iloczyn jest równy 2744,a ich największy wspólny dzielnik jest liczbą pierwszą. Czy należy te pary szukać metodą prób i błędów Dzieląc 2744 przez kolejne liczby pierwsze? To trochę nudne i pracochłonne.Proszę o pomoc. Znalazłem narazie(2,1372),(4,686),(7,392). 2.Uzasadnij ,że liczba M jest całkowita.

	1		1		1
M=		+		+...+
	√1+√4		√4+√7		√97+√100

think: z takiego rozkładu na czynniki pierwsze już sporo widać 2744 | 2 1372 | 2 686 | 2 343 | 7 49 | 7 7 | 7 1

Eta: 2/ po usunięciu niewymierności

	1−√4		√4−√7		√7−√10		√90−√97		√97−√100
M=		+		+		+....+		+
	−3		−3		−3		−3		−3

	1−√100
to: M=		= 3
	−3

c.n.u

think:

	1		1		1		1
M =		+		+		+ ... +		=
	√1 + √4		√4 + √7		√7 + √10		√97 + √100

1		√1 − √4		1		√4 − √7
	*		+		*		+
√1 + √4		√1 − √4		√4 + √7		√4 − √7

	1		√97 − √100		√1 − √4
... +		*		=		+ U{√4
	√97 + √100		√97 − √100		−3

	√97 − √100		√1 − √100		1 − 10
−√7}{−3} + ... +		} =		=		= 3 reszta
	−3		−3		−3

po drodze się po prostu skraca...

Eta: 1 min. byłam szybsza

think: tak ale Ty poszłaś na skróty kiedy ja dzielnie waliłam główną trasą

Maciek: Think co do 1 zad. to 343+49=392*7=2744 tak? ale wiem ,że 49*56=2744 −> ale jak to wywnioskować ?

think: w rozkładzie są trzy 2 i trzy 7, czyli tworzysz takie liczby aby w drugiej wystąpiła tylko jedna z nich. 2744 = 2*2*2*7*7*7 2*(2²*7³) 4*(2*7³) 7*(2³*7²) 49⁽2³*7) to będą wszystkie

think: na zasadzie części wspólnej ma być wspólny tylko jeden element 2*(2*2*7*7*7) (2*2)*(2*7*7*7) (2*2*2*7)*([P7]]*7) (2*2*2*7*7)*7 2*(2*2*7)*7*7 przypadek takiej liczy odpada, bo NWD(x,y) = 2*7 a to nie jest liczba pierwsza

think: Ty sobie jeszcze podumaj nad tym trochę, a ja w końcu idę spać, chociaż już dawno miałam iść... dobrej nocy wszyćkim

Maciek: Okey przeanalizowałem i wszystko jasne A takie coś : Który ze zbiorów A<1,2²⁰⁰⁹> czy B<2²⁰⁰⁹,2²⁰¹⁰>,zawiera więcej liczb całkowitych?Odpowiedź uzasadnij.

Maciek: Dobranoc

Anna: Do Ety ! Dobry wieczór Eta (wysłałam Ci przed chwilą odpowiedź i nie wiem, co się stało: zniknął Twój post i moja treść − więc piszę jeszcze raz). Zaglądałam tu często na chwilkę, ale widząc jedynie nieliczne zabawy zadaniami (stałych zapaleńców) i ogólne bezrobocie − zmykałam. Taki to przywilej wakacji. Ale długo już to nie potrwa i ruszymy pełną parą. Wierzę, że ABBA przetrwa. Póki co, za 4 dni lecę na kilka dni odwiedzić córkę w Brukseli. Gdy szczęśliwie wrócę − zamelduję się. Pozdrawiam serdecznie!

bzzz: Maciek zbiór A ma 2²⁰⁰⁹ elementów zbiór B ma 2²⁰¹⁰ − 2²⁰⁰⁹ + 1 elementów Napisze Ci odpowiedz |B| = |A| + 1 sam spróbuj do tego dojść, nie jest trudne tym bardzie, że Ci napisałam najistotniejsze

Maciek: Zbiór B ma 2¹ elementów + 1 czyli 3 elementy?

bzzz: liczenie elementów zioru jest podobne do liczenia stron książki jeśli zaczynamy od 1 strony a skończyliśmy na 27, to znaczy, że przeczytaliśmy 27 stron. Po jakimś czasie czytamy dalej zaczynamy od strony 28 i kończymy na 35. 28 → 1 29 → 2 30 → 3 31 → 4 32 → 5 33 → 6 34 → 7 35 → 8 stron 35 − 28 + 1 = 8 stron

bzzz: Maciek sprawdź czy 2⁴ − 2³ = 2¹ a stromotnie się zawiedziesz

Maciek:

	ax
wiem nie równa się		=ax−y
	ay

Maciek: 2(1−2⁻¹)+1

bzzz: Co kto lubi ja bym napisała po prostu 2*2³ − 2³ = 2³

Maciek: Aaa czyli te 2²⁰⁰⁹ traktujesz jak 2²⁰¹⁰ bo tam jest + 1 element?

bzzz: 2²⁰⁰⁹ − to jest pewna liczba baaardzo duża, dlatego zostawiam ją jak jest natomiast 2²⁰¹⁰ = 2*2²⁰⁰⁹ zgadzasz się?

Maciek: Oczywiście

Godzio: 2²⁰¹⁰ = 2 * 2²⁰⁰⁹ bo 2¹ * 2²⁰⁰⁹ = 2^{1 + 2009} = 2²⁰¹⁰ jeśli masz takie coś: 2 * 2²⁰⁰⁹ − 2²⁰⁰⁹ + 1 to żeby to lepiej widzieć to co zrobiła bzzz podstaw sobie: 2²⁰⁰⁹ = t 2t − t + 1 = t + 1 = 2²⁰⁰⁹ + 1 zgadza się?

Maciek: a^x*a^y=a^x+y

bzzz: dlatego zbiór B ma: 2²⁰¹⁰ − 2²⁰⁰⁹ + 1 = 2*2²⁰⁰⁹ − 2²⁰⁰⁹ + 1 = 2²⁰⁰⁹ + 1 elementów czyli |A| + 1 element

Maciek: Okey rozumiem , tylko w zadaniu nie ma mowy o tym +1 elemencie , czy to trzeba samemu wiedzieć czy wywnioskować czy jak ?

Maciek: Czy po prostu zapamiętać ,że liczba o potędze niższej o 1 jest zawsze z + 1elementem?

Godzio: To już bzzz mówiła, ale powtórzę masz zbiór od 1 do 6 no to logiczne że jest 6 elementów 1 2 3 4 5 6 ale jak masz zbiór od 5 do 10 to 10 − 5 = 5 jest nie prawidłowe 5 − 1 6 − 2 7 − 3 8 − 4 9 − 5 10 − 6 Czyli 6 elementów

Maciek: Rozumiem Godzio : Najprościej zapamiętać ,że liczba o potędze niższej o 1 ma +1 element tak jak 2²⁰⁵⁰ i 2²⁰⁴⁹ to : 2*2{2049} i 2²⁰⁴⁹+1 element.

Maciek: :2*2²⁰⁴⁹ i 2²⁰⁴⁹ + 1 element − poprawka

bzzz: Maciek tu chodzi o liczebność zbioru który nie zaczyna się od 1. Może być tak, że będziesz miał zbiór <1, 3³³⁵> i <3³³³, 3³³⁴> i co z tym fantem byś zrobił

bzzz: nie ma tutaj znaczenie potęga, że tu jest wyższa a tu niższa więc dodam 1. dodaję jeden tam gdzie 'numeracja' nie zaczyna się od 1. tak samo jak mam liczbę elementów zbioru który zaczyna się od zera <0, 2⁵> ma nie 2⁵ elementów, ale 2⁵ + 1 elementów.

Maciek: A=3³³⁵=3*3*3³³³=27³³³=9³³⁴ B=3*3³³³−3³³³+1=6³³³+1=2³³⁴+1 A−B=7³³⁴+1 tak?

bzzz: Nie , ale coraz bliżej 3³³⁵ = 3¹*3¹*3³³³ = 9*(3³³³) tego nie mozna pomnożyć chyba, że są w tej samej potędze a nie są B = 3*3³³³ − 3³³³ + 1 = 2*3³³³ + 1 A − B = 9*(3³³³) − (2*3³³³ + 1) = 7*3³³³ − 1

bzzz: możesz zawsze sprawdzić na prostym przykładzie zanim coś napiszesz np czy to jest równe 3⁴ = 3*3*3² ?=? 27²

bzzz: bo wg mnie 27² = (3³)² = 3⁶ ≠ 3⁴ Złociutki kłaniają się działania na potęgach...

Maciek: Poprosiłbym jeszcze ze 2 przykłady

bzzz: A = <0, 4²⁴>; B = <4²², 4²³>

bzzz: a więcej może Godzio Ci dopisze, a jak nie to w domu Ci coś dorzucę, bo teraz musze zacząć wyłaczać maszynerię, bo kończę pracę także do później.

Maciek: Ok,narazie

Godzio: to może ogólnie ? Który ze zbiorów A = <0, 5ⁿ> czy B = <5ⁿ⁻¹, 5ⁿ> zawiera więcej elementów ?

Maciek: B=4*4²²−4²²+1=3*4²²+1 A=4²⁴=16*4²² A−B=13*4²²+1 , A zawiera więcej liczb całkowitych.

bzzz: weź poprawkę na to, że A zaczyna się od 0 nie od 1...

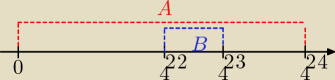
bzzz: a teraz mi powiedz czy w ogóle trzeba było to liczyć, czy wystarczyło zauważyć, że B zawiera się w A

Maciek: Wystarczyło zauważyć ... to jak będzie wygladał zbiór A jeśli jest 0 a nie 1. A=4²⁴=16*4²²−1 ?

bzzz: + 1 masz przecież o jeden element więcej niż jakbyś zaczynał od 1 zgadza się?

Maciek: Aaa.. To jakbym było np.<4,4²⁴> to A=4²⁴=16*4²²−3 ?

bzzz: 1,2,3,4,5,6 0,1,2,3,4,5,6 ile mają elementów?

Maciek:

	1		4
B=5n−5n−1=5n−5n−5−1+1=−		+1=
	5		5

A=5ⁿ+1

	1
A−B=5n+		, ale nie wiem czy to B dobrze rozpisałem.
	5

Maciek: 6 i 7 elementów.

bzzz: Maciek zastanowię się co Ty do mnie napisałeś ale naprawdę już w domu...

Maciek: Skoro <0,4²⁴> to 16*4²²+1 , <1,4²⁴> to 16*4²² , <2,4²⁴> to 16*4²²+1 czy −1?

Godzio:

	5n		1
5n−1 =		= 5n *
	5		5

A ok

	1		4
B: 5n − 5n−1 + 1 = 5n(1 −		) + 1 =		* 5n + 1
	5		5

	4		1
A − B = 5n + 1 −		* 5n + 1 =		* 5n
	5		5

I z tego wynika że A zawiera więcej elementów niż B

Maciek: O jeden element mamy mniej niż jak było <1,...> więc −1?To jak <4,...> to −3? to mnie zastanawia.

Maciek: Ach Godzio nawiasu w B nie dałem ..

Maciek: Będę później bzzz. dziękuję za dotychczasową pomoc

Godzio: <0, a> = a + 1 <1, a> = a <a, b > = b − a + 1

Maciek: Dzięki Godzio − właśnie tego mi brakowało

think: no to już wszystko jasne?

think: Maciek: Skoro <0,4²⁴> to 16*4²²+1 , <1,4²⁴> to 16*4²² , <2,4²⁴> to 16*4²²+1 czy −1? ale po co wyciągasz 16 skoro w obu przypadkach masz tą samą potęgę? To ma sens kiedy potęgi są różne także <0,4²⁴> to 4²⁴+1 , <1,4²⁴> to 4²⁴ , <2,4²⁴> to 4²⁴ − 2 + 1 ale to pewnie już wiesz po wpisie Godzia. pozdrawia bzzz po domowemu

think: i kolejny przykład do zmęczenia A = <−4, 4²⁶> ; B = <2⁵¹,2⁵³>

think: liczba elementów A = <a,b> |A| = b − a + 1 zawsze

think: jako ćwiczenie możesz spróbować z tego wyprowadzić wzorki podane przez Godzia no a w każdym razie dwa pierwsze

Maciek: B=2⁵³−2⁵¹=2*2*2⁵¹−(2⁵¹+1)=3*2⁵¹−1 A=4²⁶−(−4)+1=4²⁶+5 B−A=3*2⁵¹−1−(4²⁶+5)=3*2⁵¹−4²⁶−6 Jak to zamienić do wspólnej potęgi ?

Maciek: Ach jest błąd w B powinno być +1 i w B−A na końcu −4

think: Maciek wydawało mi się, że taki fakt jest ogólnie znany 4 = 2² (a^b)^c = a^b*c

Maciek: B−A=3*2⁵¹−(2²)²⁶−4=3*2⁵¹−2⁵²−4=3*2⁵¹−2*2⁵¹−4=2⁵¹−4 tak?

think: tak

think: może jutro dam Ci jeszcze jeden sprawdzający przykład na dziś jestem wykończona.

Maciek: Think mam kolejne zadanko ale poprosiłbym o wskazówkę: Wyznacz p wiedząc ,że:

	x		y3		x5		x
√		*√		*√		=(		)p
	y		x3		y5		y

	x5
To jest pierwiastek w pierwiastku a		jest pod 3 pierwiastkami.
	y5

Czy iść w tą stronę ,że podnosić do kwadratu i będą mi rosły potęgi po prawej stronie i będę wyjmował x i y z pod pierwiastków?

think: jak najbardziej tym bardziej, że wszędzie masz mnożenie nie dodawanie, więc będzie się to ładnie podnosić do kwadratu.

think: aczkolwiek można podziałać na potęgach bez podnoszenia do kwadratu √a = a^1/2

think: także masz dwie możliwości, proponuję posłużyć się obiema, to bardzo dobre ćwiczenie.

think: a tak na marginesie następne zadanie załóż w nowym poście, tu jest tego za dużo już.

Maciek: Ok no to działam

think: mogłam zrobić gdzieś błąd ale wydaje mi się, że to będzie dobra odpowiedź, wyszło mi p =

	3
		także działaj.
	8

Maciek:

	x89*y43		x
Ja jestem w sytuacji		=
	y89*x43		y

think: ale jaką to robiłeś metodą? podnoszenia do kwadratu?

Maciek: x do ⁹₈

Maciek: nie √2=2 do ¹₂

think: raju błąd na błędzie

x9/8
	= x...
x3/4

think:

	y3/4
tak samo		= y...
	y9/8

Maciek: =x^3/2

think:

	9		3
ile to		−
	8		4

Maciek:

3
8

Maciek:

	3
y=−
	8

think:

	x3/8		x
tak czyli masz x3/8y−3/8 =		= (		)3/8
	y3/8		y

Maciek: no to tylko końcówkę miałem źle a nie błąd na błędzie

think: hehehe ja pisałam o sobie nie o Tobie, miałeś dobrze, tylko, że nie było hmm uproszczone do końca kilka razy próbowałam napisać ten ułamek z x−ami i mi za każdym razem coś nie tak wychodziło a to klamry zapomniałam a to zamiast 9/8 napisałam 8/7... na szczęście deprymujące treści usunęłam bez śladu

Maciek:

	ax
tylko zapomniałem ,że		=ax−y
	ay

think: tutaj nie tylko z tego można dojść do tej postaci, możesz np od tej strony:

1
	= x−a
xa

	xb
więc		= xb*x−a = xb−a jest to samo a innym sposobem?
	xa

Maciek: tak jest

Maciek: Dobra dam Ci już dzisiaj spokój Dobranoc

think: Tobie również dobrej noc jutro możemy znowu przewałkować z 90 postów

Maciek: Jutro dopiero wieczorem od 21−22 bo pracuję