Zadanka Godzio: To są zadania których w ogóle nie rozumiem i nie wiem jak rozwiązać także jeśli się da to albo rozwiązanie albo jakieś mocne wskazówki . 1. Za pomocą metod rachunku różniczkowego określić liczbę rozwiązań równania: 2x³ + 1 = 6|x| − 6x² 2.Pewna firma przeprowadza co kwartał regulację płac dla swoich pracowników, waloryzując je zgodnie ze wskaźnikiem inflacji, który jest stały i wynosi 1,5% kwartalnie , oraz doliczając stałą kwotę podwyżki 16zł. W styczniu 2001 pan Kowalski otrzymał wynagrodzenie 1600 zł. Jaką pensję otrzyma w kwietniu 2002, Wyznaczyć wzór ogólny na pensję w_n pana Kowalskiego w n−tym kwartale, przyjmując w₁ = 1600 jest płacą w pierwszym kwartale 2001. Obliczyć średnią miesięczną płacę pana Kowalskiego w 2002 roku. 3.Czy można sumę 42 000 złotych podzielić na pewną liczbę nagród tak aby kwoty tych nagród wyrażały się w pełnych setkach złotych, tworzyły ciąg arytmetyczny oraz żeby najwyższa nagroda wynosiła 13 000 zł. Jeśli tak to podać liczbę i wysokość tych nagród.

b.: zadanie 1: 2. przypadki: x<0, x>0 pomaga zobaczyć wykres różnicy: http://www.wolframalpha.com/input/?i=plot+2x^3+%2B+1+-+6|x|+%2B+6x^2+%2C+x+from+-1+to+1 żeby pokazać, że jest dokładnie 1 rozw. ujemne wystarczy pokazać, że różnica rośnie na (−∞,0), i np. w −1 jest ujemna, a w 0 dodatnia żeby pokazać, że są dokładnie 2 rozw. dodatnie wystarczy pokazać, że na (0,∞) różnica najpierw maleje, a potem rośnie, oraz że wartości: w 0 i w 1 są dodatnie, a np. w 1/2 ujemna

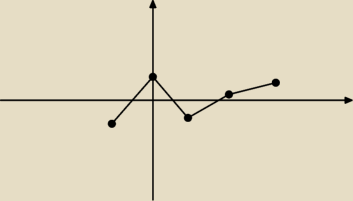Godzio: f(x) = 2x³ + 6x² − 6|x| + 1 dla x ≥ 0 f(x) = 2x³ + 6x² − 6x + 1 f(1) = 2 + 6 − 6 + 1 = 3 > 0

	1		1		3		7		1
f(		) =		+		− 3 + 1 =		− 2 = −		< 0
	2		4		2		4		4

f(0) = 1 dla x < 0 f(x) = 2x³ + 6x² + 6x + 1 f(−1) = −2 + 6 − 6 + 1 = −1 < 0 Narysowałem prowizoryczny wykres wzorując się na kolejnych wyrazach wynik jest taki że są 3 rozwiązania

bzzz: ad3 zaczynam ponownie bo poprzedni tekst mi zjadło ojj czuję, że się dziś zdenerwuję... najwyższa nagroda to 13 000, gdyby nawet były tej samej wysokości, to najmniejsze możliwe n: n = 3 3*13 000 < 42 000 odpada n = 4 4*13 000 > 42 000 ok a₁ = 100k r = 100m, bo wysokość każdej nagrody musi być wielokrotnością 100 zł.

	a1 + an
Sn =		n
	2

	a1 + 13 000
42 000 =		n /*2
	2

84 000 = (100k + 13 000)n wypisujemy dzielniki 84 000 zaczynając od 4 do czasu gdy druga liczba jest > 13 000 (n = 4) 4 * 21 000 → a₁ + 13 000 = 21 000 → a₁ = 8 000 ok jest wielokrotnością 100 a teraz czy r jest wielokrotnością 100? 8 000 + 3r = 13 000 → 3r = 5 000 odpada. (n = 5) 5 * 16 800 → a₁ = ..... r = ...... (n = 6) 6 * 14 000 → a₁ = ..... r = ...... (n = 7) 7 * 12 000 odpada bo 12 000 < 100k + 13 000

Godzio: ja już na dziś wysiadam, jestem tak wykończony jak nigdy jutro sobie to przeanalizuje