Planimetria Kamil: Prosze o szybką pomoc.Dany jest kwadrat o przekątnej długości 8 cm. Z wierzchołka kwadratu zakreślamy koło o promieniu równym długości boku kwadratu. Pole powierzchni części wspólnej kwadratu i koła jest równe: A)16π B)8π C)4√2π D)16√2π

Milka: Dlaczego ma być szybka pomoc, źle się czujesz?

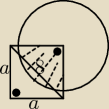
Święty: Korzystamy chocby z twierdzenia Pitagorasa. 2a²=8² a²=32 a=4√2 P=^α₃₆₀πr² P=⁹⁰₃₆₀π(4√2)² P=8π

Kamil: skad ci wyszło 8π bo nie bardzo rozumiem mozesz rozpisać prosze

Kamil: prosze o rozpisanie bede wdzięczny

Kamil: prosze o rozpisanie pola

Kamil: prosze

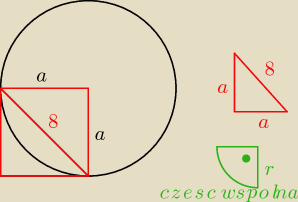
Godzio: Z Pitagorasa liczę bok kwadratu a, który jest równocześnie promieniem okręgu a² + a² = 8² 2a² = 64 /: 2 a² = 32 a = 4√2 Pole wspólne to wycinek koła o kącie 90^o Wzór na pole wycinka jest taki:

	α
Pw =		* πr2
	360

podstawiasz dane i liczysz α = 90^o , r = 4√2

	90
P =		* π * (4√2)2
	360

	1
P =		* π * 32
	4

P = 8π Święty Kamilowi trzeba wszystko dokładnie wytłumaczyć bo inaczej będzie zadawał 100 następnych pytań

Kamil: co

Zdziwiona: Co "co"? Godzio wszystko dokładnie rozpisał przecież xD