geometria kasia: Przyprostokatne Δ prostokatnego maja dł. √21 i 2.Oblicz dł. odcinków na jakie podzieliła przeciwprostokatna wysokosć poprowadzona z wierzchołka.

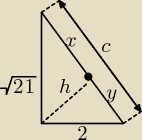
bzzz: z tw. Pitagorasa liczymy przecwiprostokątną: c² = (√21) + 2² = 21 + 4 = 25 c = 5 teraz korzystamy ze wzoru na pole:

1		1
	*2*√21 =		*h*5
2		2

	2√21
h =
	5

i ponownie z Pitagorasa: y² + h² = 2² x = c − y = 5 − y

	84		16
y2 = 4 −		=
	25		25

	4
y =
	5

	4		1
x = 5 −		= 4
	5		5

Milka: Ale dużo obliczeń! Można znacznie prościej. Długość przeciwprostokątneh x + y = √21 + 4 = 5. Korzystając z podobieństwa trójkątów otrzymujemy:

x		√21		21
	=		⇒ x =
√21		5		5

oraz

y		2		4
	=		⇒ y =
2		5		5

think: Milka, ja może jestem niedouczona, ale mnie uczono, że √21 + 2 ≠ √21 + 4

Godzio: ale tu takie coś jest : (p{21))² + 2² = (x + y)² x + y = √21 + 4 = 5

Godzio: poprawka (√21)² + 2² = (x + y)²

Milka: think − o co chodzi?