Planimetria
Kamil:
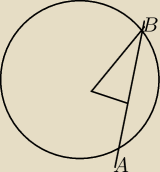
Cięciwa AB ma długość 6 dm i jest oddalona od środka koła o 2 dm.Pole koła przedstawionego na
rysunku jest równe:
A)13π dm
2
B)40π dm
2
C)3dm
2
D)25π dm
2
4 sie 17:16
Kejt:
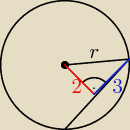
liczysz promień z twierdzenia Pitagorasa i podstawiasz do wzoru na pole ;>
4 sie 17:36
Kamil: do pola trójkąta czy koła?
4 sie 18:15
Kamil: pomóz Kejt
4 sie 18:15
Edek: wylicz r z trójkąta prostego (tw. Pitagorasa)
następnie wyliczone r podstaw do wzoru na pole koła
P=πr2 i wyjdzie Ci szukane pole koła
4 sie 18:37
Kamil: Twierdzenie Pitagorasa
32+22=r2
9+4=r2
−r=−13/:(−1)
r=13
4 sie 18:46
Kamil: Edek dobrze wyszło
4 sie 18:46
Kamil: 13=r2
r2=13 teraz dobrze
4 sie 18:49
Kamil: prosze sprawdzcie czy dobrze
4 sie 18:50
Kamil: Edek sprawdz
4 sie 18:50
Kamil: prosze cie Edek sprawdz
4 sie 18:51
Kamil: nie wiem czy zapis dobry
4 sie 18:56
Edek: dobrze r2=13 dm2, czyli Po = ...
4 sie 19:21
Kamil: Po=πr2
Po=π13
Po=13π dm2
4 sie 19:27
Maron: A skąd wiadomo że linia tworząca przyprostokątna tego trójkąta dł. 2 jest prostopadła do
cieciwy? W zadaniu nie zaznaczona kąta prostego i dlatego tak na czuja założyłem

6 kwi 16:03
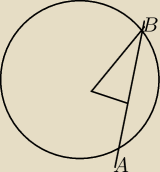 Cięciwa AB ma długość 6 dm i jest oddalona od środka koła o 2 dm.Pole koła przedstawionego na
rysunku jest równe:
A)13π dm2
B)40π dm2
C)3dm2
D)25π dm2
Cięciwa AB ma długość 6 dm i jest oddalona od środka koła o 2 dm.Pole koła przedstawionego na
rysunku jest równe:
A)13π dm2
B)40π dm2
C)3dm2
D)25π dm2
 liczysz promień z twierdzenia Pitagorasa i podstawiasz do wzoru na pole ;>
liczysz promień z twierdzenia Pitagorasa i podstawiasz do wzoru na pole ;>
