Granice Godzio: Wyznaczyć granicę ciągu:

	6√4n
an =
	√n − √n + 3√4n2

już bez tego lima pisze

6√4n		6√4n(√n + √n + 3√4n2)
	=		=
√n − √n + 3√4n2		−3√4n2

n2/3(1 + √1 + 6√n*3√4) * 6√4		1 + √1+6√n*3√4
	= −
−n2/3 * 3√4		3√4

I teraz nie wiem jak to dokończyć

think: a n do czego dąży ?

think: dobra już widzę n → ∞ no masz ładnie samo dodawanie, żadnych nieoznaczoności, licznik dąży do nieskończoności biorąc pod uwagę minus przed całością to dąży do −∞

Godzio: no właśnie tylko odpowiedź −³√4 może błąd robię ?

think: dobra sprawdzę sobie to na papiórku

think: wynik i tak mi nie wyszedł jak ten podany ale jest już bliżej

think: boshe ale mi się tego nie chce pisać no ale dla Ciebie zmogę moje lenistwo

Godzio: dziadowskie zadanie jak to mówią

Godzio: dzięki

think:

41/6n1/6
	*
n1/2 − (n + (4n2)1/3)1/2

n1/2 + (n + (4n2)1/3)1/2
	=
n1/2 + (n + (4n2)1/3)1/2

41/6(n2/3 + (n4/3 + 41/3n2/3)1/2)
	=
−41/3n2/3

−4^{1/6 − 1/3}(1 + (1 + 4^1/3n^{2/3 − 4/3})^1/2) = −4^{− 1/6}(1 + (1 + 4^1/3n^−2/3)^1/2) =

	41/3
= −4− 1/6(1 + (1 +		)1/2)
	n2/3

think: a teraz wychodzi miałam błąd w rozwiązaniu na brudno

	1		1		1
tak to jest gdy		−		jakimś cudem równa się −
	6		3		3

Godzio:

	1		1
−4−1/6(1 + (1 + 3√4p3{		)1/2		−> 0
	n2		n2

−4^−1/6 * 2 = −4^−1/6 * 4^1/2 = −4^{−1/6 + 3/6} = −4^2/6 = −4^1/3 = −³√4 Dzięki wielkie!

domino:

think: No patrz czasem mi się nawet coś udaje to była przyjemność zrobić coś i nie musieć po n razy tłumaczyć a co, a skąd, a dlaczego

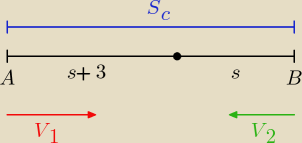
Godzio: I jeszcze zadanko do sprawdzenia bo nie jestem pewien czy dobrze rozumuje bo wynik się zgadza Dwaj rowerzyści wyruszyli jednocześnie w drogę, jeden z A do B drugi z B do A i spotkali się po jednej godzinie. Pierwszy z nich przebywał w ciągu godziny o 3 km więcej niż drugi i przyjechał do celu o 27 min wcześniej niż drugi. Jakie były prędkości obu rowerzystów i jaka jest odległość AB ? I tak : |AB| = s_c = 2s + 3

	2s + 3
v1 =
	27   t −   60

	2s + 3
v2 =
	t

I czy mogę takie coś napisać: v₁ = (s + 3)km/h v₂ = s km/h

	27
(s + 3)(t −		) = 2s + 3
	60

	2s + 3
st = 2s + 3 => t =
	s

	2s + 3		27
(s + 3)(		−		) = 2s + 3
	s		60

	9		6s + 9		27
2s + 3 −		s +		−		= 2s + 3 / − (2s + 3) / * s
	20		s		20

	9		27
−		s2 + 6s + 9 −		s = 0
	20		20

	9		93		20
−		s2 +		+ 9 = 0 / *
	20		20		3

−3s² + 31s + 60 = 0 Δ = 31² + 12 * 60 = 1681 √Δ = 41

	−31 − 41
s1 =		= 12km
	−6

s₂ < 0 |AB| = 27km v₁ = 15km/h v₂ = 12km/h

think: co prawda tego typu zadania to absolutnie nie moja brocha, ale wydaje mi się, że za bardzo nie było inaczej jak tego rozwiązać i jak dla mnie wszystko jest w porządku...

Godzio: Dobra to w takim razie już ostatnie zadanko, którego nie umiem ruszyć. Dwa punkty poruszają się ruchem jednostajnym po okręgu w tym samym kierunku, przy czym jeden z nich wyprzedza drugi co 44 sec. Jeżeli zmienić kierunek ruch jednego z tych punktów na przeciwny to będą się one spotykać co 8 sec.. Obliczyć stosunek prędkości tych punktów

domino: zad z rowerzystami:

	s+3
v1=		= s+5 [km/h]
	1

	s
v2 =		= s[km/h]
	1

t₂− t₁= ²⁷₆₀

	2s+3		2s+3		27
		−		=
	s		s+3		60

to; s= 12km => IABI= 2s+3 = 27km v₁=....... v₂=.......

think: takie luźne skojarzenie... gdy dwa obiekty poruszają się w przeciwnym kierunku to ich prędkości się dodają. gdyby zamiast tych dwóch wziąć trzeci, którego prędkość jest równa v₁ + v₂ i on wtedy robi koło w 8 sekund, a może pół koła <myśli> natomiast kiedy poruszają się w tym samym kierunku to v₂ − v₁ ale jakoś nic konkretnego

Godzio: Nie mam pojęcia jak to wykorzystać

think: a znasz chociaż odpowiedź do tego zadania?

think: a tak na marginesie widziałeś zadanie Kamila? czy tylko mnie się tak wydaje, czy nie ma tam poprawnej odpowiedzi?

Godzio:

	13
odp to
	9

think: rozwiąż takie coś

	2πr
v2 − v1 =
	44

	2πr
v2 + v1 =
	8

	v2
a na koniec
	v1

Godzio: co do Kamila to pewnie miało być tam 2√3 ale glowy nie dam

Godzio: ooo dzięki postaram się to zrozumieć

domino: v₁ −− predkość szybszego v₂ −−− prędkość słabszego v₁>v₂

	2πr
zgodnie z kierunkim : v1 −v2=
	44

	2πr
przeciwnie v1 −v2=
	8

rozwiąż układ tych równań i po "ptokach"

	v1		13
odp:		=		jest ok
	v2		9

domino: think mnie uprzedziła

think: no mnie też tak wyszło po pobieżnym rachunku w pamięci

think: domino, miałam opory, bo jakoś nie potrafię sama przez sobą tego rozwiązania uzasadnić

think: kurcze Domino, nie możesz rozwiązać zadania Lukasza? bo mnie ono męczy a sama nie potrafię, w końcu to nieprawdopodobieństwo

Godzio: Dobra jeszcze nad tym pomyślę bo nie wiem dokładnie dlaczego tak jest

Godzio: Oooo ja też nad tym zadaniem myślałem i w sumie nic nie wymyśliłem i też chętnie bym się dowiedział jak to zrobić

think: Godzio kołacze mi się po głowie, że to działa na takiej zasadzie: v₁ < v₂ w takim razie spowolnijmy oba o v₁ wtedy v₁ stanie w miejscy a v₂ będzie mijał go co 44 sekundy czyli tym samym będzie zataczał pełne koło przekonałam Cię

Godzio:

	2πr
Dobra po dogłębnej analizie zrozumiałem to: v2 − v1 =
	44

	2πr
ale to: v1 + v2 =		to juz nie wiem ehh prześpię się z tym może to coś da
	8

think: zatrzymaj v₁ w miejscu a v₂ niech leci z prędkością powiększoną o v₁, wtedy będzie zataczać pełne koło w 8 sekund

Godzio: No dobra coś już rozumiem

think: w takim razie ja brykam do

domino: To ja spadam,bo padam Dobranoc

domino: Matematycy to "nocne marki" Pewnie i Kamil będzie matematykiem