poprowadzono dwie cięciwy które

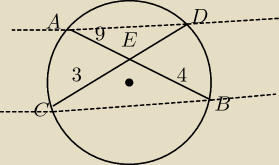
Planimetria Kamil: Godzio pomóz W okregu poprowadzono dwie cięciwy AB i CD, które przecieły się w punkcie E.Wiedząc, ze IAEI=9cm, IFBI=4cm, ICEI=3cm, oblicz IEDI.

31 lip 18:54

Kamil: nie wiem jak to zrobić, pomóz mi w zadaniu, wsokosc w tamtym zadaniu wyszła mi 4,2

31 lip 19:00

Lucyna: rysunek

Głowy nie dam ale to można z tw Talesa zrobić.

\|AE\|		\|CE\|
	=
\|EB\|		\|ED\|

31 lip 19:26

Kamil:

9		3
	=
4		x

31 lip 20:46

Lucyna: no i tylko zostaje x wyliczyć...

31 lip 21:08

Kamil: 9x=12

31 lip 21:11

Kamil: tak

31 lip 21:11

Kamil: x=12/:9

	12
x=
	9

	4
x=
	3

31 lip 21:15

Lucyna: tak... czyli x = ... ?

31 lip 21:16

Lucyna: no i ok.

31 lip 21:16

Kamil:

	1
x=1
	3

31 lip 21:17

Kamil: w ksiazce odpowiedz jest inna

31 lip 21:18

Kamil: pisze w ksiazce x=12 to chyba bład

31 lip 21:19

Lucyna: Kamil możliwe, że 12, przecież pisałam że nie daję głowy za to rozwiązanie...

31 lip 21:23

Kamil: sprawdzisz czy to dobrze i napisz zle czy dobrze ok

31 lip 21:29

Lucyna: Kamil napisz mi jeszcze raz ile ma AE = .... i te które są dane

31 lip 21:39

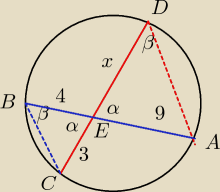
Godzio: rysunek

te 2 trójkąty są podobne więc proporcja powinna wyglądać tak:

4		3
	=
x		9

3x = 36 x = 12

31 lip 21:41

Godzio: Tutaj ( o ile się nie mylę ) nie można korzystać z Talesa bo te 2 linie ( przerywane ) nie są równoległe

31 lip 21:42

Lucyna: no i właśnie tego nie byłam pewna, dzięki Godzio emotka

planimetria to zdecydowanie nie moje ulubieństwo...

31 lip 21:51

Godzio: Tak samo jak u mnie stereometria emotka

31 lip 21:57

Gustlik: Masz rację Godzio, nie możesz korzystać z tw. Talesa, bo linie nie musza być równległe, nie pisze o tym w tresci zadania, więc nie można zrobić takiego założenia. Istnieje twierdzenie o dwóch cięciwach, w opisanym zadaniu wyglądałoby ono tak − skorzystam Godzio z Twojego rysunku: |AE|*|EB|=|CE|*|ED| (czyli obrazowo: iloczyn dwóch odcinków jednej cięciwy utworzonych przez punkt przecięcia jest równy iloczynowi dwóch odcinków drugiej cięciwy) Czyli: 3x=4*9 3x=36 /:3 x=12 To twierdzenie wzieło się z podobieńtsw ΔBCE i ADE, o których pisałeś. Pozdrawiam.***********

1 sie 15:35

Radosław 2: Do całkowitej poprawności powyższych dywagacji brakuje jeszcze uzasadnienia ,iż trójkąty(rys Godzia) EBD i ECA są podobne.A wystarczy zauważyć,że kąt ABD i kąt ACD muszą być równe bo są oparte na tym samym łuku AD i równe połowie kąta środkowego wpisanego w dany okrąg Czyli końcowa proporcja powstaje z porównania dwóch równań: ^x_sinγ=⁴_sinδ i ⁹_sinγ=³_sinδ

2 sie 08:50