pochodna Marek: W książce do matematyki znalazłem taki wzór:

	h   sin   2
limh → 0 (		) = 1
	h   2

Czy nie jest to symbol nieoznaczony [⁰₀] ?

	h		h
przecież sin		= 0 i odpowiednio		= 0
	2		2

Skąd więc bierze się powyższy wzór?

AS: Jest to podstawowe twierdzenie o granicy funkcji

	sin(a*x)
lim(x→0)		= 1
	a*x

Basia: można udowodnić, że

	sinx
limx→0		=1
	x

dowód opiera się na nierówności x<sinx<tgx co jest prawdą dla wszystkich kątów ostrych i co dość łatwo zobaczyć na odpowiednim rysunku w układzie współrzędnych spróbuj poszukać w literaturze, a jeśli nie znajdziesz napisz może uda mi się jakoś ten dowód tutaj napisać (i narysować)

Basia: ale bzdurę napisałam oczywiście sinx < x < tgx

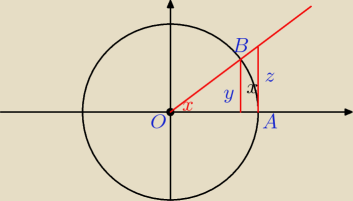Basia: okrąg ma promień r=1 jeżeli kąt ma miarę (w radianach) x to łuk AB musi mieć długość x jest więc oczywiste, że y < x < z sinx = ^y_r=y tgx = ^z_OA=z czyli sinx < x < tgx x→0⁺ to sinx>0 dzielimy przez sinx

	x		tgx		1
1<		<		=
	sinx		sinx		cosx

na mocy tw. o trzech ciagach

	x		1
limx→0+ 1 ≤ limx→0+		≤ limx→0+
	sinx		cosx

	x		1
1 ≤ limx→0+		≤		=1
	sinx		cos0

stąd:

	x
limx→0+		=1
	sinx

	sinx		1
limx→0+		= limx→0+		= 1
	x		x   sinx

dla x→0⁻ |sinx| < |x| < |tgx| a ponieważ wszystkie są wtedy ujemne to −sinx < −x < −tgx /*(−1) sinx > x > tgx x→0⁻ to sinx,0 dzielimy przez sinx i dalej jak poprzednio dowodzimy, że

	sinx
limx→0−		= 1
	x

i ostatecznie

	sinx		sinx
limx→0+		=limx→0−		= 1
	x		x

czyli

	sinx
limx→0		istnieje i
	x

	sinx
limx→0+		=1
	x